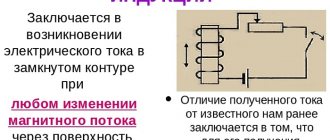
Содержание
Электрический ток представляет собой упорядоченное движение заряженных частиц. Этими частицами могут являться не только свободные электроны, но и ионы.
Металлы являются отличными проводниками. Какие частицы приходят в движение под действием электрического поля в них: электроны или ионы?
В данном уроке вы узнаете ответ на этот вопрос. Мы вспомним некоторые факты о строении металлов и рассмотрим процессы, которые будут происходить в этих веществах при протекании тока.
Строение металлов
Находясь в твердом агрегатном состоянии, металлы обладают кристаллической решеткой. Это упорядоченная структура: каждый атом находится в строго определенном месте.
Но какие частицы тогда будут обеспечивать протекание электрического тока? Дело в тем, что в узлах кристаллической решетки находятся положительные ионы (рисунок 1). В пространстве меду этими ионами беспрестанно двигаются свободные электроны.
Рисунок 1. Кристаллическая решетка металла
Вспомним немного о том, что же представляют собой такие частицы, как ионы. В обычных условиях атомы электрически нейтральны. Электроны несут отрицательный заряд, а протоны, находящиеся в ядре — положительный. Заряд этот по модулю одинаков. Таким образом, в электрически нейтральном атоме количество электронов будет равно количеству протонов в ядре.
Если атом теряет хоть один электрон, он теряет свою электронную стабильность. Теперь суммарный положительный заряд всех протонов в ядре по абсолютному значению больше отрицательного заряда электронов. Такой атом называют положительным ионом.
В таком строении кроется ответ на вопрос: “Почему в обычных условиях металл электрически нейтрален?”.
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решетки.
Обратите внимание на тот факт, что не все электроны в металлах являются свободными. Часть из них остается связанными с ядрами атомов, а другая их часть — беспорядочно движется между этими атомами.
Эти электроны изначально находятся на самых удаленных от ядра орбитах. Они слабо связаны с ядром. Поэтому они могут довольно легко переходить от одного атома к другому, повторяя этот процесс множество раз. Именно это движение мы и называем беспорядочным движением свободных электронов.
Учебники
Варламов А. Как в металле протекает электрический ток? // Квант. – 1995. – № 1. – С. 37-38.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Этот вопрос обычно не вызывает затруднений у школьников. Как протекает? Да очень просто. Если между концам проводника, например металлического, поддерживать разность потенциалов, то в нем возникает электрическое поле. Действуя на имеющиеся в металле свободные электроны, это поле придает им ускорение в направлении того конца проводчика, потенциал которого выше (заряд электронов отрицательный). Возникает направленное движение зарядов, которое и является электрическим током.
Нельзя сказать, что такой ответ ошибочен. Все слова в нем верны. Однако этот, на первый взгляд исчерпывающий ответ сразу же вызывает целый ряд других вопросов и возражений. Попробуем и них разобраться.
Как движутся электроны при создании между концами проводника разности потенциалов? Казалось бы, ускоренно, ведь на них все время действует сила \( \vec F = e \cdot \vec E\) (\( \vec E\) – напряженность электрического поля в проводнике). Но, с другой стороны, если бы это действительно было так, то сила тока в любом сечении проводника со временем возрастала бы, что противоречит закону Ома – при постоянном напряжении сила тока, протекающего по проводнику, постоянна\ . Как же быть? Вспомним о внутреннем устройстве металла.
Валентные электроны атомов металлов связаны с атомами весьма слабо. Поэтому при образовании кристаллической решетки они легко отрываются от атомов к образуют довольно плотный электронный газ (даже если от каждого атома оторвется лишь по одному электрону, то их концентрация в таком газе окажется порядка n
~ 1029 м3, в чем вы можете убедиться самостоятельно). Рассуждая выше о протекании тока через металл, мы считали эти электроны свободными. В определенном смысле это верно, но не следует забывать и об их окружении – ионной кристаллической решетке.
Созданная в конце XIX – начале XX веков классическая электронная теория сопротивления металлов предполагала, что в процессе движения под действием электрического поля электроны сталкиваются с ионами кристаллической решетки. Среди этих столкновения бывают и такие, при которых электроны всю приобретенную при разгоне в электрическом поле энергию передают решетке. Именно такие столкновения, их называют эффективными
, и ответственны за сопротивление металла. Остальные столкновения для понимания механизма протекания тока можно не принимать в расчет (после них изменяется лишь направление скорости электронов, но не ее величина).
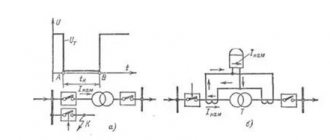
Пусть среднее время между соударениями есть τ. Тогда можно представить себе следующую модель движения электрона в металле, в котором создано электрическое поле. В интервале времени от 0 до τ электрон движется с ускорением \( \vec a = \dfrac {e \cdot \vec E}{m}\), и, следовательно, проекция скорости его направленного движения против поля \( \vec E\) линейно возрастает со временем\[ \upsilon = a \cdot t = \dfrac {e \cdot E \cdot t}{m}\]. В момент времени τ электрон сталкивается с ионом и полностью передает кинетическую энергию своего направленного движения решетке. Далее он снова ускоряется электрическим полем, и процесс повторяется. График зависимости проекции скорости упорядоченного движения от времени приведен на рисунке 1.
Рис. 1
Такое кусочно-равноускоренное движение можно представить себе как равномерный дрейф электрона в направлении, противоположном полю, со скоростью \( \upsilon_{cp} = \dfrac {e \cdot E \cdot \tau}{2m}\). Вычислим связанную с этим движением силу тока.
Число электронов, проходящих через сечение S
проводника за время Δ
t
, есть \( \Delta N = n \cdot S \cdot \upsilon_{cp} \cdot \Delta t\). При этом перекосится заряд \( \Delta q = e \cdot \Delta N = n \cdot e \cdot S \cdot \upsilon_{cp} \cdot \Delta t\). Следовательно, в проводнике протекает ток
\( I = \dfrac {\Delta q}{\Delta t} = n \cdot e \cdot S \cdot \upsilon_{cp} = n \cdot S \cdot \dfrac {e^2 \cdot \tau}{2m} \cdot E \).
Величина \( j = \dfrac {I}{S} = \dfrac {n \cdot e^2 \cdot \tau}{2m}\cdot E\). называется плотностью тока.
Оказывается, полученный нами коэффициент при напряженности поля Е
, который составлен только из микроскопических характеристик металла, есть не что иное, как величина, обратная удельному сопротивлению металла ρ.
Ну вот, кое-что стало проясняться. Однако вопросы еще остались. Давайте, например, оценим среднюю скорость направленного движения электронов. Пусть по медному проводнику сечением, скажем 10 мм2 и концентрацией электронов n
= 1,67∙1029 м-3 протекает ток I = 10 А. Тогда средняя скорость
\( \upsilon_{cp} = \dfrac {I}{n \cdot e \cdot S} \approx \) 0,04 мм/с.
Если же по известному из эксперимента значению ρ определить время между эффективными соударениями, то окажется, что τ ~ 10-14 с. Поэтому, если предполагать, что пробег между эффективными соударениями происходит со средней скоростью υcp ~ 0,1 мм/с, то мы приходим к абсурдному утверждению: расстояние между двумя соударениями электрона составляет \(l = \upsilon_{cp} \cdot \tau \sim \) 10-18 м, что на много порядков меньше расстояния: между ближайшими нонами в решетке. Следовательно, мы снова чего-то не учли.
А не учли мы того, что частицы электронного газа в металле, подобно молекулам идеального газа в сосуде, находятся в постоянном хаотическом движении. Однако, если воспользоваться такой аналогией и вместо υcp подставить в выражение для l
тепловую скорость \(\upsilon_{t} = \sqrt{\dfrac{3k \cdot T}{m}}\), то этого все равно окажется недостаточно для согласия с опытными данными (убедитесь в этом самостоятельно).
Мы исчерпали возможности классической физики. В действительности последовательная теория сопротивления металлов была построена только в середине XX века с помощью представлений квантовой физики. Оказалось, что электроны в металле движутся с гигантскими скоростями υe ~ 0,01с
(
с
– скорость света в вакууме). Это хаотическое движение частиц электронного газа имеет чисто квантовое, а не тепловое происхождение – оно не прекращается даже при абсолютном нуле температуры. Но и при столь огромных скоростях хаотического движения электронов в отсутствие электрического поля средний перенос заряда через выделенное сечение проводника равен нулю. При включении электрическою поля на это хаотическое движение накладывается упорядоченный дрейф электронов против поля – как это уже было описано выше. Расстояние же между двумя последовательными соударениями определяется именно большой скоростью хаотического движения и составляет для взятого нами конкретного медного проводника несколько десятков (а может бить, даже сотен) межатомных расстояний, что уже вполне правдоподобно.
И, наконец, последняя неожиданность. Согласно законам квантовой механики, электрон в идеальной периодической кристаллической решетке двигается так, что он… никогда не сталкивается с ионами, ее образующими. А как же быть тогда со всеми нашими предыдущими умозрительными построениями? Как же тогда электроны при своем движении в кристалле передают свою энергию решетке?
Оказывается, при низких температурах электроны сталкиваются с примесными атомами и другими дефектами, всегда имеющимися а решетке реального кристалла. Устраняя их, сопротивление кристаллического металлов можно делать все меньше и меньше. При комнатных же температурах электроны в основном рассеиваются на… колебаниях решетки. Если в неподвижной решетке они еще могли «строить» свое поведение так, чтобы «обойти» все периодически повторяющиеся ионы, то когда последние совершают тепловые колебания, электроны уже никак не могут «уследить» за их хаотическим движением и неизбежно сталкиваются то с одним, то с другим.
Вот, вкратце, какие «подводные камни» встретились нам при внимательном рассмотрении, казалось бы, такого ясного вопроса.
Ток в металлах
Создадим в металле электрическое поле с помощью любого источника тока. Положительные ионы останутся в узлах кристаллической решетки. В движение придут именно свободные электроны под действием электрических сил. Их движение станет направленным (рисунок 2).
Рисунок 2. Ток в металле
При этом сохранится и беспорядочность этого движения. Как это можно представить? Вообразите себе стайку мошкары, где каждое насекомое беспорядочно двигается. Если подует ветер, то эта стайка начнет перемещаться в одном направлении, при этом беспорядочное движение внутри этой стайки сохранится. На это и будет похоже движение электронов под действием электрических сил.
Теперь мы можем определить природу электрического тока в металлах и дать ему определение.
Электрический ток в металлах — это упорядоченное движение свободных электронов.
Формула расчета
Точный расчёт удельного заряда (em) в металлах можно определить по следующей формуле:
Em=lu0Rq
Где:
- l — сила тока, мгновенно возникающая в проводнике при остановке катушки;
- u 0 — начальная линейная скорость витков проволоки;
- R — сопротивление цепи;
- q — заряд.
Проведение опытов Р. Толменом и Б. Стюартом позволили упорядочить ранее полученные сведения от других учёных. Несмотря на это, электрические проводники активно использовались в электрических изделиях с начала XIX века, доказательство электронной природы тока в металлах, позволило ускорить появление сложных устройств.
Доказательные опыты
Сделанные нами выводы построены не просто на рассуждениях, но и множество раз доказаны эмпирически. Российские ученые Леонид Исаакович Мандельштам (рисунок 3) и Николай Дмитриевич Папалекси (рисунок 4) провели ряд интересных опытов. Эти опыты позже были подтверждены американскими физиками Бальфуром Стюартом и Робертом Толменом.
Рисунок 3. Леонид Исаакович Мандельштам (1879 — 1944) — российский и советский физик, один из основателей научной школы радиофизики
Рисунок 4. Николай Дмитриевич Папалекси (1880 — 1947) — российский и советский физик, основоположник радиоастрономии
Суть опытов заключалась в следующем. Уже известно, что в металле есть какие-то свободные заряды, и они обладают массой. Тогда они должны испытывать на себе инерцию.
Для проверки этого предположения металлический проводник нужно было привести в движение, а затем резко остановить. Для удобства использовали вращательно движение, а не поступательное.
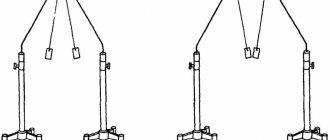
Металлическую проволоку наматывали на деревянный каркас и раскручивали (рисунок 5). После резкой остановки с помощью гальванометра фиксировали возникновение тока.
Рисунок 5. Опыт Мандельштама и Папалекси
Было определено, что именно электроны вылетали из проводника. Установили это, определяя отношение заряда к массе его носителя. Эти данные для электрона у ученых уже имелись.
Опыт Мандельштама и Папалекси
Электронную природу тока в металле первыми экспериментально доказали российские физики Мандельштам и Папалекси в 1913 г. Для того, чтобы выяснить, какие частицы создают электрический ток в металлах, они — без подключения внешнего источника — регистрировали ток в катушке из металлического провода, которую сначала сильно раскручивали вокруг собственной оси, а затем резко останавливали. Поскольку у электрона есть масса, то он должен подчиняться закону инерции. Поэтому в момент остановки атомы решетки останутся на месте, а свободные электроны по инерции, какое-то время, продолжат движение в прежнем направлении. То есть в цепи должен появиться электрический ток. Эксперименты подтвердил это предположение — после остановки катушки исследователи регистрировали бросок тока в цепи.
Рис. 2. Опыт Мандельштама и Папалекси.
Этот эксперимент в 1916 г. повторили американцы Стюарт и Толмен. Им удалось повысить точность измерений и получить отношение заряда электрона eэ к значению массы электрона mэ:
$$ {e_э \over m_э } = 1,8*10^{11} Кл/кг $$
Этот фундаментальный результат совпал с полученными данными из других экспериментов, поставленных на основе измерения других параметров. Впервые эту величину в 1897 г. измерил англичанин Джозеф Томсон по отклонению пучка электронов в зависимости от напряженности электрического поля.
Скорость распространения электрического поля и тока в металлах
После создания электрического поля свободные электроны приходят в движение. Скорость их движения совсем небольшая. В среднем она составляет несколько миллиметров в секунду.
Но как тогда после щелчка выключателем лампа в комнате загорается мгновенно? Дело обстоит в следующем.
Именно само электрическое поле распространяется в проводнике с огромной скоростью. Она близка к скорости света в вакууме ($c = 300 \space 000 \frac{км}{с}$). Распространяется поле по всей длине проводника.
Соответственно, в движение приходят одновременно все электроны в проводнике. И те, что ближе к выключателю, и те, что ближе к электроприбору.
Например, пошлем электрический сигнал из Владивостока в Москву. Расстояние между этими городами составляет около 8000 км. В Москве сигнал будет зафиксирован уже через 0,03 с. Это не означает, что электроны от Владивостока проделали весь этот путь за указанное время и прибыли в Москву. Нет, это электрическое поле распространилось по проводам с невероятной скоростью и привело в движение самые ближние к приемнику в Москве электроны в движение, которое и было зафиксировано.
Поэтому, когда говорят о скорости распространения тока в проводнике, то имеется в виду скорость распространения электрического поля по всей длине проводника.
Что такое металлы?
«Металлом называется светлое тело, которое ковать можно»,— писал в 1763 году Ломоносов. Загляните в ваш учебник химии и вы увидите, что металлы обладают характерным металлическим блеском («светлое тело»), хорошо проводят тепло и электрический ток. Правда, тут же вы прочтете, что существуют элементы, проявляющие свойства как металлов, так и неметаллов. Другими словами, нет четкой грани, отделяющей одно от другого. Химика, который интересуется, в первую очередь, химическими реакциями и для которого каждый элемент — свой особый мир, такая неоднозначность не очень смущает. А вот физика это не устраивает. Если физика делит тела на металлы и неметаллы, то нужно понять, в чем их принципиальное различие. Поэтому надо так определить, что такое металл, чтобы, как и в других случаях в области точных наук, удовлетворить двум требованиям:
- все металлы должны обладать всеми без исключения приписываемыми им признаками;
- иные объекты должны не обладать хотя бы одним из этих признаков.
Вооружившись этими соображениями, посмотрим, все ли металлы без исключения имеют все свойства, приписываемые им учебником. Начнем с «ковать можно», т. е. с пластичности, говоря современным языком. И тут же, по созвучию, мы вспомним пластмассы: ведь не зря они так названы, многим из них свойственна пластичность — способность необратимо изменять форму без разрушения. Конечно, медь, железо, алюминий ковать легко, со свинцом еще проще, индий — довольно редкий и дорогой металл — можно мять почти как воск (а воск ведь — не металл!), щелочные металлы и того мягче. А попробуйте стукнуть по обычному чугуну — и он разлетится на кусочки! Ну, тут металлурги скажут: это потому, что чугун — не простое вещество. Он состоит из кристаллов железа, разделенных прослойками углерода, т. е. графита. Вот по этим-то прослойкам чугун и ломается. Ну что же, все верно. Только вот беда — хрупкий графит, как оказывается, современная физика относит к металлам! Да и не один графит: числятся, например, среди металлов мышьяк, сурьма и висмут, но ковать их можно с таким же успехом, как стекло — разлетаются на мелкие кусочки!
Проделайте такой простой опыт: разбейте баллон сгоревшей лампы, достаньте оттуда вольфрамовую спираль и попробуйте ее раскрутить. Ничего не выйдет, она рассыпется в пыль! Но ведь как-то ее сумели скрутить на заводе? Значит, может быть и такое — то можно деформировать, то нельзя, в зависимости от того, что происходило с образцом в прошлом. Что ж, придется, видимо, с этим признаком — пластичностью — расстаться. Тем более, что он присущ многим неметаллам; ведь то же стекло — нагрей его, и оно станет мягким и податливым.
Итак, укорачиваем формулировку и двигаемся дальше.
На очереди — «блеск», или, говоря научным языком, оптические свойства. Блестящих предметов много: и вода, и стекло, и полированные камни, да мало ли что еще. Так что просто «блеском» не обойтись, вот и говорится: для металлов характерен металлический блеск. Ну, это совсем хорошо: получается, что металл — это металл. Правда, интуитивно мы чувствуем, что металлическим блеском блестят полированные медь, золото, серебро, железо. А широко распространенный минерал пирит — разве не блестит, как металлы? Про типичные полупроводники германий и кремний и говорить не приходится, по внешнему виду их от металлов никак не отличишь. С другой стороны, не так давно научились получать хорошие кристаллы таких соединений, как двуокись молибдена; кристаллы эти коричнево-фиолетовые и на обычный металл мало похожи. Оказывается, это вещество надо считать металлом. Почему — будет ясно чуть дальше.
Так что блеск как чисто «металлический» признак отпадает.
На очереди — теплопроводность. Пожалуй, этот признак можно отбросить сразу — все без исключения тела проводят тепло. Правда, про металлы говорится, что они хорошо
проводят тепло. Но, боюсь, на вопрос «что такое хорошо и что такое плохо?» в этом случае ни один папа не ответит.
Хорошо ли проводит тепло медь? Посмотрим в таблицу и сразу же столкнемся со встречным вопросом: а какая медь и при какой температуре? Если взять чистую медь, например ту, из которой делают провода для радиоприборов, и нагреть ее до красного каления, т. е. отжечь, то при комнатной температуре она да еще чистое серебро будут проводить тепло лучше любого другого металла. Но погните такой медный образец, стукните или зажмите в тисках — и его теплопроводность станет заметно хуже. А что произойдет, если кусочек отожженной меди начать охлаждать? Сначала теплопроводность будет расти, увеличится в десятки раз при температуре около 10 К, а потом начнет быстро падать и при достижении абсолютного нуля должна стать нулевой (рис. 1).
Рис. 1. Зависимость удельной теплопроводности от температуры для различных веществ. (Удельная теплопроводность — это количество теплоты, которое протекает между противоположными гранями кубика со стороной 1 см при разности температур между этими гранями 1 К в 1 с.)
Возьмем теперь другой металл — висмут. Картина для него очень похожа на ту, которую мы видели для меди, только максимум теплопроводности лежит при 3 К, а при комнатной температуре висмут проводит тепло плохо, не многим лучше, чем кристалл кварца. Но кварц-то — не металл! И тот же кварц, как видно из рисунка 1, по своим теплопроводным свойствам иногда оказывается не хуже меди. А плавленный кварц, т. е. кварцевое стекло, проводит тепло плохо, примерно как нержавеющая сталь.
Кварц — не исключение. Все кристаллы хорошего качества ведут себя подобным образом, только числа будут немного различными. У алмаза, например, уже при комнатной температуре теплопроводность лучше, чем у меди.
Отбрасываем с чистым сердцем теплопроводность и жалеть об этом не будем. И не только потому, что по этому признаку металл от неметалла не так уж легко отличить, но и потому, что, оказывается, специфические черты в теплопроводности металлов (а такие есть) являются следствием его электропроводности — последнего оставшегося свойства.
И опять в формулировке, приведенной в начале статьи, уточнение — не просто электропроводность, а хорошая
электропроводность. А ведь когда речь шла о теплопроводности, эпитет «хорошая» нас насторожил и, как оказалось, не напрасно. Что же — и последнее свойство под подозрением? Надо обязательно его спасать, а то мы останемся вообще без металлов, а заодно без полупроводников, без изоляторов. Вот это наука получается! Любой школьник в большинстве случаев не задумываясь скажет, с чем он имеет дело, а копнули поглубже — остановились в недоумении.
И есть от чего. Возьмем таблицы физических величин и посмотрим на числа. Вот, к примеру, при комнатной температуре удельное сопротивление ρ
(Ом·см) меди ~1,55·10-6; у висмута
ρ
~ 10-4; у графита
ρ
~ 10-3; у чистых кремния и германия
ρ
~ 102 (но, добавляя примеси, его можно довести до ~10-3); у мрамора
ρ
= 107 — 1011; у стекла
ρ
= 1010; а где-то в конце списка — янтарь с удельным сопротивлением до 1019. И где же тут кончаются металлы-проводники и начинаются диэлектрики? А мы еще не упомянули про электролиты. Обычная морская вода неплохо проводит ток. Что же — и ее считать металлом?
Посмотрим, не поможет ли нам температура. Если повышать температуру, то различия между веществами начнут сглаживаться: у меди сопротивление начнет расти, у стекла, например, уменьшаться. Значит, надо проследить за тем, что произойдет при охлаждении. И вот тут мы наконец увидим качественные различия. Посмотрите на рисунок 2: при температурах жидкого гелия, вблизи абсолютного нуля, вещества разделились на две группы. У одних сопротивление остается небольшим, у сплавов или у не очень чистых металлов ρ
почти не изменяется при охлаждении, у чистых металлов сопротивление сильно уменьшается. Чем чище и совершеннее кристалл, тем значительнее это изменение. Иногда ц при температуре, близкой к абсолютному нулю, меньше, чем при комнатной, в сотни тысяч раз. У других веществ, например у полупроводников, с понижением температуры сопротивление начинает стремительно возрастать, и чем ниже температура, тем оно больше. Бели бы можно было добраться до абсолютного нуля, то
ρ
стало бы бесконечно большим. Впрочем, достаточно и того, что сопротивление реально становится столь большим, что никаким современным прибором его уже не измеришь.
Итак, мы добрались до ответа: металлы — это такие вещества, которые проводят электричество при любой температуре.
Рис. 2. Зависимость удельного сопротивления чистых металлов (меди и платины) и полупроводника (чистого германия) от температуры.
В противоположность этому диэлектрики перестают проводить ток, если их охладить до абсолютного нуля. Если пользоваться таким определением, то и графит, и двуокись молибдена оказываются металлами. А куда же отнести полупроводники? Если речь идет о чистых, совершенных кристаллах, то они, строго говоря, диэлектрики. Но если в них содержится много примесей, то они могут стать металлами, т. е. сохранять проводимость при самых низких температурах.
Что же у нас осталось в конце концов? Нам удалось выявить единственный
существенный признак, руководствуясь которым мы можем, если не в повседневной практике, то хотя бы в принципе, всегда отличить металл от неметалла. А раз этот признак единственный, то оказываются автоматически удовлетворенными оба условия, выполнения которых мы потребовали в начале статьи.