При проектировании электрических схем, инженеры сталкиваются с тем, что проводники обладают определенным сопротивлением, на которое оказывают влияния температурные колебания. Статья даст подробное описание, что такое зависимость сопротивления от температуры и как температура влияет на проводимость различных веществ — металлов, газов и жидкостей. Дополнительно будет приведена формула расчета такой зависимости.
Сопротивление
Сопротивлением называется способность проводника пропускать через себя электрический ток. Единицей измерения данной физической величины является Ом. На принципиальных схемах эта величина обозначается буквой «R». На величину сопротивления любого проводника электрическому току влияет его структура. Двигаясь внутри структуры, свободные электроны сталкиваются с атомами и электронами, которые замедляют их движение. Чем их концентрация больше, тем выше будет само электрическое сопротивление.
О способности проводников проводит электрический ток судят по величине его удельного сопротивления. Удельное сопротивление проводника — это сопротивление протеканию тока через проводник из любого вещества с площадью поперечного сечения 1 м² и длиной один метр. Обозначается в физике данная величина буквой «ρ». Данный параметр является табличной величиной и измеряется в системе СИ как Ом×м (может также измеряться в Ом×см и Ом×мм²/м).
Жаропрочные и жаростойкие стали
По своим электропроводящим свойствам жаропрочные и жаростойкие стали близки к хромоникелевым. Высокое содержание в этих сплавах хрома и никеля не позволяет им проводить электрический ток, подобно обычным углеродистым с высокой концентрацией железа.
Значительное удельное электросопротивление и высокая рабочая температура таких сталей делают возможным их применение в качестве рабочих элементов электрических нагревателей. В частности, сталь 20Х23Н18 по своему сопротивлению и жаростойкости в некоторых случаях способна заменить такой популярный сплав для нагревателей, как нихром Х20Н80. Удельное электрическое сопротивление жаропрочных и жаростойких сталей ρэ·108, Ом·м
| Температура, °С | 15Х25Т (ЭИ439) | 15Х28 (ЭИ349) | 40Х9С2 (ЭСХ8) | Х25С3Н (ЭИ261) | 20Х23Н18 (ЭИ 417) | Х20Н35 |
| — | — | — | — | — | 106 | |
| 20 | — | — | 75 | 80 | — | — |
| 100 | — | — | — | — | 97 | — |
| 200 | — | — | — | — | 98 | 113 |
| 400 | 102 | — | — | — | 105 | 120 |
| 600 | 113 | — | — | — | 115 | 124 |
| 800 | — | 122 | — | — | 121 | 128 |
| 900 | — | — | — | — | 123 | — |
| 1000 | — | 127 | — | — | — | 132 |
- Казанцев Е. И. Промышленные печи. Справочное руководство для расчетов и проектирования.
- Физические величины. Справочник. Под ред. И. С. Григорьева, Е. З. Мейлихова. — М.: Энергоатомиздат, 1991. — 1232 с.
Сверхпроводимость
Снижение температуры металлических проводников сильно увеличивает их проводимость. Это связано с тем, что в структуре вещества замедляется движение атомов и электронов, благодаря чему снижается вероятность их столкновения со свободными электронами. При температуре абсолютного 0 (–273 градуса Цельсия) возникает явление падения до нуля сопротивления проводника. Зависимость сопротивления проводника от температуры при абсолютном 0 — сверхпроводимость.
Температура, при которой обычный проводник становится сверхпроводником, называется критической. Она будет разной для различных чистых металлов и сплавов. Все будет зависеть от их структуры, химического состава и структуры кристаллов. Например, серое олово с алмазной структурой является полупроводником. Но белое олово при своей тетрагональной кристаллической ячейке, мягкости и плавкости, переходит в состояние сверхпроводника при температуре 3.70 К. Также при критической температуре прослеживается целый ряд других способностей:
- Повышение частоты переменного тока вызывает рост сопротивления, значение гармоник с периодом световой волны.
- Способность удерживать величину силы тока ранее приложенного, а затем отключенного источника.
Металл или сплав может перейти в состояние сверхпроводника и при нагревании. Такое явление называют высокотемпературной проводимостью. Ответ на вопрос, почему от высокой температуры сопротивление металлов снижается, может довольно просто объяснить их кристаллическая структура. В момент нагрева до критических значений, электроны перестают хаотично перемещаться внутри структуры вещества. Они выстраиваются в цепочку. Такое построение не мешает движению свободных электронов, а значит падает общее сопротивление. Переход в состояние высокотемпературной проводимости начинается с порога 1000К и этот показатель выше, чем точка кипения азота.
Температурная зависимость ρ(Т)
Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.
Удельное сопротивление металлов и сплавов, Ом*мм2/м
(при Т = 200С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 200С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (6),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность или .
Рис. 2. Температурная зависимость удельного сопротивления проводника
В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.
Рис. 3. Справочные значения температурного коэффициента удельного сопротивления проводников
Применение
Свойство проводников изменять сопротивление при определённой температуре используют для создания различных элементов электрических схем и измерительных приборов. О них будет рассказано далее в данной статье.
Резистор
Сопротивление устройств старого типа сильно зависело от их нагрева. При нагревании проводимость резистора пропорционально изменялась в меньшую сторону. Для электрических цепей требуется идеальный резистор, который обладает наивысшим коэффициентом проводимости. Для снижения нагрева при производстве данных устройств теперь используется материал, имеющий малую зависимость сопротивления от температуры нагрева. Это позволило применять резисторы с малым сопротивлением для цепей с большим напряжением.
Терморезистор
Существует отдельная группа резисторов, которые применяют для измерения температуры. Особенностью такого устройства является то, что он может снижать свою проводимость при нагреве. При этом он отключает цепь при достижении определенного порогового значения.
Термометр сопротивления
Это прибор был разработан для измерения температуры среды. Он состоит из тонкой платиновой проволоки, защитного чехла и корпуса. Прибор имеет стабильную реакцию на перепады температуры. Измеряемой величиной в данном устройстве служит сопротивление этой проволоки из платины. Чем выше будет температура, тем сопротивление соответственно будет больше. Понижение сопротивления так же фиксируется, так как в этот момент меняются проводимость и сопротивление. Для измерения температуры термометром сопротивления, в настоящее время применяются проволочные индикаторы из разнообразных металлов. В зависимости от свойств используемого металла, погрешность устройства может составлять не более 0.1 %. Благодаря этому достигается очень высокая точность измерения температуры.
Газ
Самый известный нам газовый проводник — это люминесцентная лампа. Газ нагревается за счет увеличения напряжения между анодом и катодом лампы.
Известным жидкостным проводником является щелочной аккумулятор. При понижении температуры нарушается структура жидкости и изменяется ее сопротивление.
Нагрев провоцирует движение атомов и электронов, увеличивая сопротивление и зарядный ток устройства.
Термины
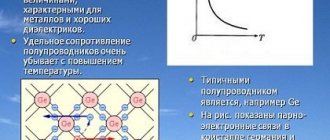
- Полупроводник – вещество с электрическими свойствами, которые характеризируют его как хорошего проводника или изолятора.
- Температурный коэффициент удельного сопротивления – эмпирическая величина (α), описывающая изменение сопротивления или удельного сопротивления с температурным показателем.
- Удельное сопротивление – степень, с которой материал сопротивляется электрическому потоку.
Сопротивление материалов основывается на температуре, поэтому получается проследить зависимость удельного сопротивления от температуры. Некоторые способны стать сверхпроводниками (нулевое сопротивление) при очень низких температурах, а другие – при высоких. Скорость вибрации атомов повышается на больших дистанциях, поэтому перемещающиеся сквозь металл электроны чаще сталкиваются и повышают сопротивление. Удельное сопротивление меняется с изменением температуры ΔT:
Сопротивление конкретного образца ртути достигает нуля при крайне низком температурном показателе (4.2 К). Если показатель выше этой отметки, то наблюдается внезапный скачек сопротивления, а далее практически линейный рост с температурой
p = p (1 + αΔT), где ρ – исходное удельное сопротивление, а α – температурный коэффициент удельного сопротивления. При серьезных переменах температуры α способно меняться, а для поиска p возможно потребуется нелинейное уравнение. Именно поэтому иногда оставляют суффикс температуры, при которой изменилось вещество (к примеру, α15).
Стоит отметить, что α положительно для металлов, а удельное сопротивление растет вместе с температурным показателем. Обычно температурный коэффициент составляет +3 × 10-3 К-1 до +6 × 10-3 К-1 для металлов с примерно комнатной температурой. Есть сплавы, которые разрабатывают специально, чтобы снизить зависимость от температуры. Например, у манганина α приближено к нулю.
Не забывайте также, что α выступает отрицательным для полупроводников, то есть, их удельное сопротивление уменьшается с ростом температурной отметки. Это отличные проводники при высоких температурах, потому что повышенное температурное смешивание увеличивает количество свободных зарядов, доступных для транспортировки тока.
Сопротивление объекта также основывается на температуре, так как R располагается в прямой пропорциональности p. Мы знаем, что для цилиндра R = ρL/A. Если L и A сильно не изменяются с температурой, то R обладает одинаковой температурной зависимостью с ρ. Выходит:
Особенности сопротивления проводников
R = R (1 + αΔT), где R – исходное сопротивление, а R – сопротивление после изменения температуры T.
Давайте рассмотрим сопротивление датчика температуры. Очень многие термометры функционируют по этой схеме. Наиболее распространенный пример – термистор. Это полупроводниковый кристалл с сильной зависимостью от температуры. Устройство небольшое, поэтому быстро переходит в тепловой баланс с человеческой частью, к которой прикасается.
Термометры основаны на автоматическом измерении температурного сопротивления термистора
Обзор
Электрический ток Батарея Измерения тока и напряжения в цепях Микроскопический вид: скорость дрейфа
Сопротивление и резисторы Закон Ома Температура и сверхпроводимость Сопротивление и удельное сопротивление Зависимость сопротивления от температуры
Электрическая энергия и энергия
Переменные токи Фазоры Средниеквадратное значение корня Меры предосторожности в домашнем хозяйстве
Активное и индуктивное сопротивление кабелей
Электричество в мире Люди и электрическая опасность Проводимость нервов и электрокардиограммы Электрическая активность в сердце
Как повысить силу электрического тока. Сопротивление проводников. Удельное сопротивление
Закон Ома является самым главным в электротехнике. Именно поэтому электрики говорят: «- Кто не знает Закон Ома, пусть сидит дома». Согласно этому закону ток прямо пропорционален напряжению и обратно пропорционален сопротивлению ( I = U / R ), где R является коэффициентом, которое связывает напряжение и силу тока.
Единица измерения напряжения – Вольт, сопротивления – Ом, силы тока – Ампер.
Для того, чтобы показать, как работает Закон Ома, разберем простую электрическую цепь. Цепью является резистор, он же – нагрузка. Для регистрации на нем напряжения используется вольтметр. Для тока нагрузки – амперметр. При замыкании ключа ток идет через нагрузку. Смотрим, насколько соблюдается Закон Ома. Ток в цепи равен: напряжение цепи 2 Вольта и сопротивление цепи 2 Ома ( I = 2 В / 2 Ом =1 А). Амперметр столько и показывает. Резистор является нагрузкой, сопротивлением 2 Ома. Когда замыкаем ключ S1, ток течет через нагрузку. С помощью амперметра измеряем ток цепи. С помощью вольтметра – напряжение на зажимах нагрузки. Ток в цепи равен: 2 Вольта / 2 Ом = 1 А. Как видно это соблюдается.
Теперь разберемся, что нужно сделать, чтобы поднять силу тока в цепи. Для начала увеличиваем напряжение. Сделаем батарею не 2 В, а 12 В. Вольтметр будет показывать 12 В. Что будет показывать амперметр? 12 В/ 2 Ом = 6 А. То есть, повысив напряжение на нагрузке в 6 раз, получили повышение силы тока в 6 раз.
Рассмотрим еще один способ, как поднять ток в цепи. Можно уменьшить сопротивление – вместо нагрузки 2 Ом, возьмем 1 Ом. Что получаем: 2 Вольта / 1 Ом = 2 А. То есть, уменьшив сопротивление нагрузки в 2 раза, увеличили ток в 2 раза. Для того, чтобы легко запомнить формулу Закона Ома придумали треугольник Ома: Как можно по этому треугольнику определять ток? I = U / R. Все выглядит достаточно наглядно. С помощью треугольника также можно написать производные от Закона Ома формулы: R = U / I; U = I * R. Главное запомнить, что напряжение находится в вершине треугольника.
В 18 веке, когда был открыт закон, атомная физика находилась в зачаточном состоянии. Поэтому Георг Ом считал, что проводник представляет собой что-то, похожее на трубу, в которой течет жидкость. Только жидкость в виде электротока. При этом он обнаружил закономерность, что сопротивление проводника становится значительнее при увеличении его длины и меньше при увеличении диаметра.
Исходя из этого, Георг Ом вывел формулу: R = p *l / S,
где p – это некоторый коэффициент, умноженный на длину проводника и деленный на площадь сечения. Этот коэффициент был назван удельным сопротивлением, характеризующим способность создавать препятствие протеканию эл.тока, и зависит из какого материала изготовлен проводник. Причем, чем больше удельное сопротивление, тем больше сопротивление проводника. Чтобы увеличить сопротивление необходимо увеличить длину проводника, либо уменьшить его диаметр, либо выбрать материал с большим значением данного параметра. В частности, для меди удельное сопротивление составляет 0,017 ( Ом * мм2 / м ).
Зависимость сопротивления платинового термосопротивления от температуры
Для промышленных платиновых термометров сопротивления используется уравнение Каллендара-Ван Дьюзена (en), с известными коэффициентами, которые установлены экспериментально и нормированы в стандарте DIN EN 60751-2009 (ГОСТ 6651-2009):
RT=R1+AT+BT2+CT3(T−100)(−200∘C RT=R1+AT+BT2(∘C≤T<850∘C),{\displaystyle R_{T}=R_{0}\left\;(0\;{}^{\circ }\mathrm {C} \leq T<850\;{}^{\circ }\mathrm {C} ),} здесь RT{\displaystyle R_{T}} — сопротивление при температуре T{\displaystyle T} °C, R{\displaystyle R_{0}} сопротивление при 0 °C, A,B,C{\displaystyle A,B,C} — коэффициенты — константы, нормированные стандартом: A=3.9083×10−3∘C−1{\displaystyle A=3.9083\times 10^{-3}\;{}^{\circ }\mathrm {C} ^{-1}} B=−5.775×10−7∘C−2{\displaystyle B=-5.775\times 10^{-7}\;{}^{\circ }\mathrm {C} ^{-2}} C=−4.183×10−12∘C−4.{\displaystyle C=-4.183\times 10^{-12}\;{}^{\circ }\mathrm {C} ^{-4}.}
Поскольку коэффициенты B{\displaystyle B} и C{\displaystyle C} относительно малы, сопротивление растёт практически линейно при увеличении температуры.
Для платиновых термометров повышенной точности и эталонных термометров выполняется индивидуальная градуировка в ряде температурных реперных точек и определяются индивидуальные коэффициенты вышеприведенной зависимости.
Факторы, влияющие на сопротивление полупроводников
Опытным путем было установлено, что при повышении температуры происходит уменьшение электрического сопротивления в полупроводниковых кристаллах. Это связано с тем, что при нагревании кристалла увеличивается количество свободных электронов, соответственно, возрастает их концентрация. Изменяющееся сопротивление полупроводников под воздействием температуры, применяется для создания специальных приборов, называемых терморезисторами.
Для того, чтобы изготовить терморезистор используются полупроводники, представляющие собой оксиды отдельных металлов в смешанном состоянии. Готовое вещество размещается в защитном металлическом корпусе с изолированными выводами. С их помощью происходит подключение прибора к электрической цепи.
Терморезисторы используются для измерения температуры или для ее поддержания в заданном режиме в каких-либо устройствах. Основным принципом их работы является изменяющееся сопротивление при перепадах температур. Тот же принцип используется и в фоторезисторах. Здесь величина сопротивления изменяется в зависимости от уровня освещения.
Полупроводники
А как зависит сопротивление от нагрева в полупроводниках? Для начала поговорим о терморезисторах. Это такие устройства, которые меняют свое электрическое сопротивление под воздействием тепла. У данного полупроводника температурный коэффициент сопротивления (ТКС) на порядок выше металлов. Как положительные, так и отрицательные проводники, они имеют определенные характеристики.
Где: 1 – это ТКС меньше нуля; 2 – ТКС больше нуля.
Чтобы такие проводники, как терморезисторы приступили к работе, за основу берут любую точку на ВАХ:
- если температура элемента меньше нуля, то такие проводники используются в качестве реле;
- чтобы контролировать изменяющийся ток, а также, какая температура и напряжение, используют линейный участок.
Терморезисторы применяются, когда осуществляется проверка и замер электромагнитных излучений, что осуществляются на сверхвысоких частотах. Благодаря этому данные проводники используют в таких системах, как пожарной сигнализации, проверке тепла и контроль употребления сыпучих сред и жидкостей. Те терморезисторы, у которых ТКС меньше нуля, применяются в системах охлаждения.
Теперь о термоэлементах. Как влияет явление Зеебека на термоэлементы? Зависимость заключается в том, что такие проводники функционируют на основе данного явления. Когда температура места соединения повышается при нагревании, на стыке замкнутой цепи появляется ЭДС. Таким образом, проявляется их зависимость и тепловая энергия обращается в электричество. Чтобы полностью понять процесс, рекомендую изучить нашу инструкцию о том, .
Такое устройство носит название термопары. Термоэлементы применяются как источники тока малой мощности, а также для измерения температур цифрового вычислительного прибора, у которых размеры должны быть маленькие, а показания точные.
Подробнее о полупроводниках, и влияние нагрева на их сопротивление рассказывается на видео:
Ну и последнее, о чем хотелось бы рассказать — холодильники и полупроводниковые нагреватели. Полупроводниковые спаи обеспечивают в конструкции разность температур до шестидесяти градусов. Благодаря этому и был сконструирован холодильный шкаф. Температура охлаждения в такой камере достигает – 16 градусов. В основу работы элементов лежит применение термоэлементов, через которые проходит электрический ток.
В своей практической деятельности каждый электрик встречается с разными условиями прохождения носителей зарядов в металлах, полупроводниках, газах и жидкостях. На величину тока влияет электрическое сопротивление, которое различным образом изменяется под влиянием окружающей среды.
Одним из таких факторов является температурное воздействие. Поскольку оно значительно изменяет условия протекания тока, то учитывается конструкторами в производстве электрооборудования. Электротехнический персонал, участвующий в обслуживании и эксплуатации электроустановок, обязан грамотно использовать эти особенности в практической работе.
Влияние температуры на электрическое сопротивление металлов
В школьном курсе физики предлагается провести такой опыт: взять амперметр, батарейку, отрезок проволоки, соединительные провода и горелку. Вместо амперметра с батарейкой можно подключить омметр или использовать его режим в мультиметре.
Теперь поднесем пламя горелки к проволоке и станем ее нагревать. Если смотреть на амперметр, то будет видно, что стрелка станет перемещаться влево и достигнет положения, отмеченного красным цветом.
Результат опыта демонстрирует, что при нагревании металлов их проводимость уменьшается, а сопротивление возрастает.
Математическое обоснование этого явления приведено формулами прямо на картинке. В нижнем выражении хорошо видно, что электрическое сопротивление «R» металлического проводника прямо пропорционально его температуре «Т» и зависит еще от нескольких параметров.
Как нагрев металлов ограничивает электрический ток на практике
Лампы накаливания
Ежедневно при включении освещения мы встречаемся с проявлением этого свойства у ламп накаливания. Проведем несложные измерения на лампочке с мощностью 60 ватт.
Самым простым омметром, питающемся от низковольтной батарейки 4,5 V, замерим сопротивление между контактами цоколя и увидим значение 59 Ом. Этой величиной обладает нить накала в холодном состоянии.
Вкрутим лампочку в патрон и через амперметр подключим к ней напряжение домашней сети 220 вольт. Стрелка амперметра покажет 0,273 ампера. По определим сопротивление нити в нагретом состоянии. Оно составит 896 Ом и превысит предыдущее показание омметра в 15,2 раза.
Такое превышение предохраняет металл тела накала от перегорания и разрушения, обеспечивая его длительную работоспособность под напряжением.
Переходные процессы при включении
При работе нити накала на ней создается тепловой баланс между нагревом от проходящего электрического тока и отводом части тепла в окружающую среду. Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Переходные процессы протекают за короткое время и вызваны тем, что скорость возрастания электрического сопротивления от нагрева металла не успевает за увеличением тока. После их окончания устанавливается рабочий режим.
Во время длительного свечения лампы постепенно толщина ее нити доходит до критического состояния, которое приводит к перегоранию. Чаще всего этот момент возникает при очередном новом включении.
Для продления ресурса лампы различными способами уменьшают этот бросок тока, используя:
1. устройства, обеспечивающие плавную подачу и снятие напряжения;
2. схемы последовательного подключения к нити накала резисторов, полупроводников или терморезисторов (термисторов).
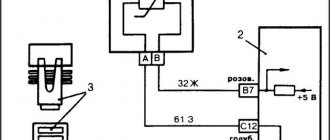
Пример одного из способов ограничения пускового тока для автомобильных светильников показан на картинке ниже.
Здесь ток на лампочку подается после включения тумблера SA через предохранитель FU и ограничивается резистором R, у которого номинал подбирается так, чтобы бросок тока во время переходных процессов не превышал номинальное значение.
При нагреве нити накала ее сопротивление возрастает, что ведет к увеличению разности потенциалов на ее контактах и параллельно подключенной обмотке реле KL1. Когда напряжение достигнет величины уставки реле, то нормально открытый контакт KL1 замкнется и зашунтирует резистор. Через лампочку начнет протекать рабочий ток уже установившегося режима.
Влияние температуры металла на его электрическое сопротивление используется в работе измерительных приборов. Их называют .
Их чувствительный элемент выполняют тонкой проволочкой из металла, сопротивление которой тщательно замерено при определенных температурах. Эту нить монтируют в корпусе со стабильными термическими свойствами и закрывают защитным чехлом. Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
На выводы чувствительного элемента монтируются провода электрической схемы, которыми подключается цепь замера сопротивления. Его величина пересчитывается в значения температуры на основе ранее произведенной калибровки прибора.
Бареттер — стабилизатор тока
Так называют прибор, состоящий из стеклянного герметичного баллона с газообразным водородом и металлической проволочной спиралью из железа, вольфрама или платины. Эта конструкция по внешнему виду напоминает лампочку накаливания, но она обладает специфической вольт-амперной нелинейной характеристикой.
На ВАХ в определенном ее диапазоне образуется рабочая зона, которая не зависит от колебаний приложенного на тело накала напряжения. На этом участке бареттер хорошо компенсирует пульсации питания и работает в качестве стабилизатора тока на подключенной последовательно к нему нагрузке.
Работа бареттера основана на свойстве тепловой инерции тела накала, которая обеспечивается маленьким сечением нити и высокой теплопроводностью окружающего ее водорода. За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
Это основное отличие бареттера от осветительных ламп накаливания, в которых для поддержания яркости свечения стремятся уменьшить конвективные потери тепла с нити.
Сверхпроводимость
В обычных условиях среды при охлаждении металлического проводника происходит уменьшение его электрического сопротивления.
При достижении критической температуры, близкой к нулю градусов по системе измерения Кельвина, происходит резкое падение сопротивления до нулевого значения. На правой картинке показана такая зависимость для ртути.
Это явление, названное сверхпроводимостью, считается перспективной областью для исследований с целью создания материалов, способных значительно снизить потери электроэнергии при ее передаче на огромные расстояния.
Однако, продолжающиеся изучения сверхпроводимости выявили ряд закономерностей, когда на электрическое сопротивление металла, находящегося в области критических температур, влияют другие факторы. В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
Влияние температуры на электрическое сопротивление/проводимость газов
Газы и обычный воздух являются диэлектриками и не проводят электрический ток. Для его образования нужны носители зарядов, которыми выступают ионы, образующиеся в результате воздействия внешних факторов.
Нагрев способен вызвать ионизацию и движение ионов от одного полюса среды к другому. Убедиться в этом можно на примере простого опыта. Возьмем то же оборудование, которым пользовались для определения влияния нагрева на сопротивление металлического проводника, только вместо проволоки к проводам подключим две металлические пластины, разделенные воздушным пространством.
Подсоединенный к схеме амперметр покажет отсутствие тока. Если между пластинами поместить пламя горелки, то стрелка прибора отклонится от нулевого значения и покажет величину проходящего через газовую среду тока.
Таким образом установили, что в газах при нагревании происходит ионизация, приводящая к движению электрически заряженных частиц и снижению сопротивления среды.
На значении тока сказывается мощность внешнего приложенного источника напряжения и разность потенциалов между его контактами. Она способна при больших значениях пробить изоляционный слой газов. Характерным проявлением подобного случая в природе является естественный разряд молнии во время грозы.
Примерный вид вольт-амперной характеристики протекания тока в газах показан на графике.
На начальном этапе под действие температуры и разности потенциалов наблюдается рост ионизации и прохождение тока примерно по линейному закону. Затем кривая приобретает горизонтальное направление, когда увеличение напряжения не вызывает рост тока.
Третий этап пробоя наступает тогда, когда высокая энергия приложенного поля так разгоняет ионы, что они начинают соударяться с нейтральными молекулами, массово образуя из них новые носители зарядов. В результате ток резко возрастает, образуя пробой диэлектрического слоя.
Практическое использование проводимости газов
Явление протекания тока через газы используется в радиоэлектронных лампах и люминесцентных светильниках.
Для этого внутри герметичного стеклянного баллона с инертным газом располагают два электрода:
1. анод;
2. катод.
У люминесцентной лампы они выполнены в виде нитей накала, которые разогреваются при включении для создания термоэлектронной эмиссии. Внутренняя поверхность колбы покрыта слоем люминофора. Он излучает видимый нами спектр света, образующийся при инфракрасном облучении, исходящем от паров ртути, бомбардируемых потоком электронов.
Ток газового разряда возникает при приложении напряжения определенной величины между электродами, расположенными по разным концам колбы.
Когда одна из нитей накала перегорит, то на этом электроде нарушится электронная эмиссия и лампа гореть не будет. Однако, если увеличить разность потенциалов между катодом и анодом, то снова возникнет газовый разряд внутри колбы и свечение люминофора возобновится.
Это позволяет использовать светодиодные колбы с нарушенными нитями накала и продлять их ресурс работы. Только следует учитывать, что при этом в несколько раз надо поднять на ней напряжение, А это значительно повышает потребляемую мощность и риски безопасного использования.
Влияние температуры на электрическое сопротивление жидкостей
Прохождение тока в жидкостях создается в основном за счет движения катионов и анионов под действием приложенного извне электрического поля. Лишь незначительную часть проводимости обеспечивают электроны.
Влияние температуры на величину электрического сопротивления жидкого электролита описывается формулой, приведенной на картинке. Поскольку в ней значение температурного коэффициента α всегда отрицательно, то с увеличением нагрева проводимость возрастает, а сопротивление падает так, как показано на графике.
Это явление необходимо учитывать при зарядке жидкостных автомобильных (и не только) аккумуляторных батарей.
Влияние температуры на электрическое сопротивление полупроводников
Изменение свойств полупроводниковых материалов под воздействием температуры позволило использовать их в качестве:
- термических сопротивлений;
термоэлементов;
холодильников;
нагревателей.
Терморезисторы
Таким названием обозначают полупроводниковые приборы, изменяющие свое электрическое сопротивление под влиянием тепла. Их значительно выше, чем у металлов.
Величина ТКС у полупроводников может иметь положительное или отрицательное значение. По этому параметру их разделяют на позитивные «РТС» и негативные «NTC» термисторы. Они обладают различными характеристиками.
Для работы терморезистора выбирают одну из точек на его вольт-амперной характеристике:
- линейный участок применяют для контроля температуры либо компенсации изменяющихся токов или напряжений;
нисходящая ветвь ВАХ у элементов с ТКС
Применение релейного терморезистора удобно при контроле или измерениях процессов электромагнитных излучений, происходящих на сверхвысоких частотах. Это обеспечило их использование в системах:
1. контроля тепла;
2. пожарной сигнализации;
3. регулирования расхода сыпучих сред и жидкостей.
Кремниевые терморезисторы с маленьким ТКС>0 используют в системах охлаждения и стабилизации температуры транзисторов.
Термоэлементы
Эти полупроводники работают на основе явления Зеебека: при нагреве спаянного места двух разрозненных металлов на стыке замкнутой цепи возникает ЭДС. Таким способом они превращают тепловую энергию в электричество.
Конструкцию из двух таких элементов называют термопарой. Ее КПД лежит в пределах 7÷10%.
Термоэлементы используют в измерителях температур цифровых вычислительных устройств, требующих миниатюрные габариты и высокую точность показаний, а также в качестве маломощных источников тока.
Полупроводниковые нагреватели и холодильники
Они работают за счет обратного использования термоэлементов, через которые пропускают электрический ток. При этом на одном месте спая происходит его нагрев, а на противоположном — охлаждение.
Полупроводниковые спаи на основе селена, висмута, сурьмы, теллура позволяют обеспечить разность температур в термоэлементе до 60 градусов. Это позволило создать конструкцию холодильного шкафа из полупроводников с температурой в камере охлаждения до -16 градусов.
Сопротивление металлов связано с тем, что электроны, движущиеся в проводнике, взаимодействуют с ионами кристаллической решетки и теряют при этом часть энергии, которую они приобретают в электрическом поле.
Опыт показывает, что сопротивление металлов зависит от температуры. Каждое вещество можно характеризовать постоянной для него величиной, называемой температурным коэффициентом сопротивления α
.
Этот коэффициент равен относительному изменению удельного сопротивления проводника при его нагревании на 1 К: α =
где ρ 0 — удельное сопротивление при температуре T 0 = 273 К (0°С), ρ — удельное сопротивление при данной температуре T. Отсюда зависимость удельного сопротивления металлического проводника от температуры выражается линейной функцией: ρ = ρ 0 (1+ αT).
Зависимость сопротивления от температуры выражается такой же функцией:
R = R 0 (1+ αT).
Температурные коэффициенты сопротивления чистых металлов сравнительно мало отличаются друготдруга и примерно равны 0,004 K -1 . Изменение сопротивления проводников при изменении температуры приводит к тому, что их вольт-амперная характеристика не линейна. Это особенно заметно в тех случаях, когда температура проводников значительно изменяется, например при работе лампы накаливания. На рисунке приведена ее вольт — амперная характеристика. Как видно из рисунка, сила тока в этом случае не прямо пропорциональна напряжению. Не следует, однако, думать, что этот вывод противоречит закону Ома. Зависимость, сформулированная в законе Ома, справедлива только при постоянном сопротивлении.
Зависимость сопротивления металлических проводников от температуры используют в различных измерительных и автоматических устройствах. Наиболее важным из них является
термометр сопротивления
. Основной частью термометра сопротивления служит платиновая проволока, намотанная на керамический каркас. Проволоку помещают в среду, температуру которой нужно определить. Измеряя сопротивление этой проволоки и зная ее сопротивление при t 0 = 0 °С (т. е.
R 0),
рассчитывают по последней формуле температуру среды.
Сверхпроводимость.
Однако до конца XIX в. нельзя было проверить, как зависит сопротивление проводников от температуры в области очень низких температур. Только в начале XX в. голландскому ученому Г. Камерлинг-Оннесу удалось превратить в жидкое состояние наиболее трудно конденсируемый газ — гелий. Температура кипения жидкого гелия равна 4,2 К. Это и дало возможность измерить сопротивление некоторых чистых металлов при их охлаждении до очень низкой температуры.
В 1911г работа Камерлинг-Оннеса завершилась крупнейшим открытием. Исследуя сопротивление ртути при ее постоянном охлаждении, он обнаружил, что при температуре 4,12 К сопротивление ртути скачком падало до нуля. В дальнейшем ему удалось это же явление наблюдать и у ряда других металлов при их охлаждении до температур, близких к абсолютному нулю. Явление полной потери металлом электрического сопротивления при определенной температуре получило название сверхпроводимости.
Не все материалы могут стать сверхпроводниками, но их число достаточно велико. Однако у многих из них было обнаружено свойство, которое значительно препятствовало их применению. Выяснилось, что у большинства чистых металлов сверхпроводимость исчезает, когда они находятся в сильном магнитном поле. Поэтому, когда по сверхпроводнику течет значительный ток, он создает вокруг себя магнитное поле и сверхпроводимость в нем исчезает. Всё же это препятствие оказалось преодолимым: было выяснено, что некоторые сплавы, например ниобия и циркония, ниобия и титана и др., обладают свойством сохранять свою сверхпроводимость при больших значениях силы тока. Это позволило более широко использовать сверхпроводимость.
Сопротивление проводников зависит от вещества, из которого они из-готовлены, и их геометрических размеров
R =
ρ .l /S,
где ρ
— удельное сопротивление вещества, из которого изготовлен проводник;
l
—длина проводника;
S —
площадь попереч-ного сечения проводника.
Сопротивление проводников входит в за-кон Ома для однородного участка цепи I =
U /R
, из которого и может быть определено
R =U /I
.
Из последней формулы выходит, что со-противление проводника постоянно, посколь-ку, в соответствии с законом Ома, во сколь-ко раз увеличиваем напряжение на концах проводника, во столько же раз возрастает и сила тока в нем.
Но на практике можно наблюдать и дру-гие явления. Составим электрическую цепь, схема которой показана на рис. 7.2. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, напри-мер автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напря-жение U 1
и отмечаем силу тока
I 1 .
Если теперь увеличить напряжение, например в 2 раза
(U 2 =
2
U 1),
то по закону Ома и сила тока должна увеличиться в 2 раза (
I 2
= 2
I 1).
Однако амперметр показывает силу тока значительно меньшую, чем 2
I 1
. Следова-тельно, в данном случае
закон Ома не вы-полняется.
Возникло несоответствие между вашими предшествующими знаниями и новым для вас фактом — закон Ома не всегда справед-лив. Такое несоответствие в науке назы-вается проблемой.
Проблема
(гр. — задача, затруд-нение) — сложный теоретиче-ский или практический вопрос, требующий решения.
Можно высказывать разные предположе-ния, что является попыткой объяснить на-блюдаемое явление. Однако в ходе опыта бро-сается в глаза, что при увеличенном напря-жении лампа светится ярче, чем в первом слу-чае. Это является свидетельством того, что тем-пература спирали лампы во втором случае вы-ше, чем в первом. Возможно, именно измене-ние температуры является причиной изменения сопротивления металлической спирали лампы.
Как же можно проверить такое предпо-ложение (гипотезу)? Составляем электриче-скую цепь (рис. 7.3), в которой есть метал-лический проводник в виде спирали, на-пример пружинка от шариковой ручки, и устанавливаем в цепи ток определенной си-лы. Нагревая спираль в пламени свечи или спички, заметим:
при нагревании спирали и при постоянном напряжении сила тока в цепи уменьшается, что свидетельствует об увеличении сопротивления спирали при по-вышении ее температуры.
Тщательные исследования показывают, что сопротивление металлических проводников зависит от их температуры практически ли-нейно
R =
R 0 (
1
+αt°),
где R 0
— сопротивле-ние проводника при 0 °C или +20 °C (это удобнее для техники). График такой зави-симости представлен на рис. 7.4.
Если иметь в виду, что размеры металлов при нагревании изменяются мало, то со-ответствующую формулу можно записать и для удельного сопротивления металлических проводников
ρ =
ρ 0 (
1
+αt°).
Рассмотрим, что означает коэффициент в полученных формулах. Если при 0°C со-противление проводника R 0 ,
а при
t°
C со-противление его
R,
то относительное изме-нение сопротивления, как показывает эксперимент,
(R —R 0) /R 0 =αt°
C. Материал с сайта
Коэффициент пропорциональности назы-вается температурным коэффициентом со-противления
, который характеризует зави-симость сопротивления вещества от его тем-пературы.
Температурный коэффициент сопро-тивления
равен относительному изменению сопротивления проводника при изменении его температуры на 1 К.
Для всех металлических проводников α
> 0 и мало зависит от тем-пературы.
Почему же возрастает сопротивление ме-таллических проводников с повышением температуры? Дело в том, что при нагре-вании металла возрастает интенсивность ко-лебаний ионов кристаллической решетки и скорость хаотического движения электро-нов.
Электроны чаще сталкиваются с ионами, что и уменьшает скорость их направленного движения, которое и является электричес-ким током.
В технике зависимость сопротивления металлических проводников от температуры используется в термометрах сопротивления.
Датчик температуры (например, платиновая проволочка) устанавливается в тех точках, где необходимо измерять температуру, а его сопротивление измеряют омметром, шкала которого градуируется в единицах темпера-туры. Таких датчиков, при необходимости, может быть любое количество, а измери-тельный прибор — один.
На этой странице материал по темам:
График зависимости сопротивления от температуры в вакууме
Зависимость сопротивления от температуры для вакуума
Зависимость сопротивления в вакууме от температуры
Зависимость сопротивления металлических проводников от температуры
Жидкости
Проводники тока в жидкости – это анионы и катионы, которые движутся за счет электрического внешнего поля. Электроны обеспечивают незначительную проводимость. Рассмотрим зависимость сопротивления от температуры в жидкостях.
где:
- Электролит
- Батарея
- Амперметр
Зависимость воздействия электролитов от нагревания прописывает формула:
Где а – отрицательный температурный коэффициент.
Как зависит R от нагрева (t) показано на графике ниже:
Такая зависимость должна учитываться, когда осуществляется зарядка аккумуляторов и батарей.
Металлы
Как температура влияет на металлы? Чтобы узнать эту зависимость был проведен такой эксперимент: батарейку, амперметр, проволоку и горелку соединяют между собой с помощью проводов. Затем необходимо замерить показание тока в цепи. После того как показания были сняты, нужно горелку поднести к проволоке и нагреть ее. При нагревании проволоки видно, что сопротивление возрастает, а проводимость металла уменьшается.
где:
- Металлическая проволока
- Батарея
- Амперметр
Зависимость указывается и обосновывается формулами:
Из этих формул следует, что R проводника определяется по формуле:
Пример зависимости сопротивления металлов от температуры предоставлен на видео:
Также нужно уделить внимание такому свойству, как сверхпроводимость. Если условия окружающей среды обычные, то охлаждаясь, проводники уменьшают свое сопротивление
График ниже показывает, как зависит температура и удельное сопротивление в ртути.
Сверхпроводимость – это явление, которое возникает, когда материалом достигается критическая температура (по Кельвину ближе к нулю), при которой сопротивление резко уменьшается до нуля.
Как узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности
После этого измерить намотанную часть проводника, и разделить значение на количество витков.
Вычисление площади сечения