Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
Полная мощность и ее составляющие
Электрическая мощность (P) в физике – это мера, показывающая, как быстро происходит трансформация или передача электричества. Единица измерений – ватт (Вт, W). Значение P зависит от напряжения (U) и тока (I) в замкнутой цепи.
Для постоянного тока потребляемая нагрузкой P — это результат произведения тока и напряжения:
P = I*U (А*В = Вт).
P в цепи не изменяющегося тока
Внимание! В этом случае значения обеих электрических характеристик постоянны, значит, в каждую секунду времени их величины мгновенны.
Формула меняет вид, если в цепи присутствует источник электродвижущей силы E (ЭДС):
P = I*E.
Цепям, где ток меняет свои значения периодически по синусоиде, такая формула не подходит. Вычислять P необходимо, опираясь на её мгновенные значения во временном интервале.
Полная мощность S по своему значению соответствует выражению:
S = U*I,
где:
- U – разность потенциалов на зажимах, (В);
- I – ток, (А).
Для обозначения S используют внесистемную единицу B*A (V*A).
Нагрузки, включенные в схемы с меняющимся током, могут быть:
- активными;
- реактивными: ёмкостными или индуктивными.
Активная нагрузка (АН)
Подобной нагрузкой являются элементы приборов, имеющие активное сопротивление. Рабочая часть подобных аппаратов при прохождении через них электричества нагревается.
Ток, проходя через нагрузку, совершает работу, которая затрачивается на нагревание и выделение тепловой энергии. В чем измеряется такая нагрузка? Её измеряют в омах (Ом).
К примерам АН относятся: утюг, электроплита, спирали фена, нить накала лампы, резистивное сопротивление.
К сведению. АН ведёт себя одинаково, как при постоянном, так и при изменяющемся во времени токе.
Пример АН
Емкостная нагрузка
Устройства, способные запасаться энергией в электрическом поле и создавать рециркуляцию (полный или частичный возврат) мощности, именуют ёмкостной нагрузкой. Емкостная нагрузка (ЕН) при переменном напряжении, пропуская ток, сдвигает его фазу на 900 вперёд.
Основными элементами, относящимися к ЕН, считаются:
- конденсаторы;
- кабельные линии (ёмкость между жилами);
- ЛЭП (линии электропередач) сверхвысокого напряжения;
- генераторы, работающие в режиме перевозбуждения.
ЕН отдаёт реактивную мощность (Q).
Цепь с конденсатором
Индуктивная нагрузка (ИН)
Нагрузка, в которой ток сдвинут по фазе назад от напряжения на 900, называется индуктивной. Она также потребляет Q.
Цепь с катушкой
При включении в сеть переменного напряжения катушки индуктивности (дросселя), у которой низкое активное сопротивление, в ней образуется ЭДС. Электродвижущая сила противостоит приложенному напряжению.
Важно! В случае чистой индуктивности L сопротивление синусоидальному току увеличивается с ростом частоты. Выделяемая на такой нагрузке средняя мощность P равна нулю.
Примерами ИН служат:
- асинхронные двигатели;
- электромагниты;
- дроссели;
- реакторы;
- трансформаторы;
- выпрямители.
Сюда же можно отнести тиристорные преобразователи.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
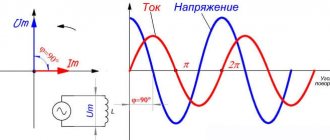
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.
Рис. 1. Сдвиг фаз индуктивной нагрузкой
Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Треугольник мощностей и cos φ
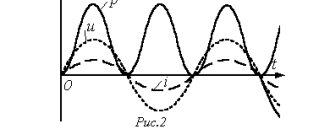
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.
Рис. 2. коэффициент мощности
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Реактивная составляющая
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Источник реактивной энергии
Чтобы понять природу появления этой энергии и то, как найти реактивную мощность, нужно уточнить, что любая электромагнитная или индукционная машина, которая работает на переменном токе, преобразует электричество в тепло. Чтобы это преобразование произошло, нужно магнитное поле. Оно, соответственно, формируется безваттной энергией. Причина в поглощении энергии индукционной цепи и отдаче ее обратно при спаде магнитного поля два раза за цикл мощностной частоты.
Природа явления
Виды энергии
Ниже представлены основные виды нагрузок, которые используются в повседневной жизни. Они могут быть как в бытовых приборах, как и в различных двигателях или датчиках.
Активная
Для данной работы используется закон Ома, который выполняется в каждую секунду времени и схож с правилом для переменного тока. Такой тип применяется в лампах для освещения или в электроплитах.
Вам это будет интересно Как воздействует электрический ток на организм человека
Активно емкостная нагрузка формула
Емкостная
Этот вид превращает в течении определенного времени энергию электрического тока в электрополе, а далее превращает ее в электрический ток. А также, здесь сила тока будет опережать напряжение.
В качестве примера может быть конденсатор. К сожалению, встретить полные реактивные нагрузки невозможно ни в одном приборе. Каждый вид не имеет коэффициент полезного действия 100%, потому что существуют потери энергии в воздухе и прочее. Потому чаще всего используется название активно-реактивной работы.
Индуктивная
Данный вид превращает энергию в магнитное поле, а далее меняет ее в электрический ток. Сила тока в этом случае будет отставать от напряжения. Для примера можно взять индуктивную катушку или датчик дросселя на автомобиле.
Функционирование выпрямителей
Зачем нужна
Электричество передает энергию в проводник для осуществления технического процесса. Чтобы процесс происходил, переданная сила должна преобразовываться в тепло и напряжение. При этом электроэнергия должна поступать постоянно, что обеспечивается обеими разновидностями мощностной характеристики. Активно действующая дает полезную силу, а реактивно действующая ее поддерживает в электродвигательных, трансформаторных, печных, сварочных, дроссельных и осветительных установках.
Активная нагрузка
К устройствам с активной нагрузкой причисляются нагревательные приборы (утюги, электроплиты, лампы накаливания, электрические чайники). Подобные приборы вырабатывают тепло и свет. Они не содержат индуктивности и емкости. Активная нагрузка преобразовывает электроэнергию в свет и тепло.
Реактивная нагрузка содержит емкость и индуктивность. Данные параметры имеют качество собирать энергию, а потом отдавать ее в сеть. Примером может служить электродвигатель, электрическая мясорубка, бытовой инструмент (пылесос, кухонный комбайн). То есть, все устройства, которые содержат электродвигатели.
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
Будет интересно➡ Что такое статическое электричество и как от него избавиться. Что вызывает статическое электричество?
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
Q = U⋅I⋅sinφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Еще раз про мощность: активную, реактивную, полную (P, Q, S), а также коэффициент мощности (PF)
Из письма клиента: Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт. Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
Мощность не всех приборов указана в Вт, например:
- Мощность трансформаторов указывается в ВА: https://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение) https://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение)
- Мощность конденсаторов указывается в Варах: https://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение) https://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение)
- Примеры других нагрузок — см. приложения ниже.
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
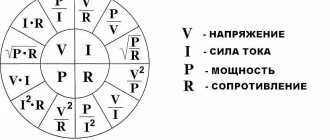
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ: https://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение) https://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение) (примеры технических данных разных нагрузок см. приложение ниже)
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский , 2004.
2. Немцов М. В. Электротехника и электроника. — М.: Издательский , 2007.
3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
Так же см. AC power, Power factor, Electrical resistance, Reactance https://en.wikipedia.org (перевод: https://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА https://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
https://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
| Однофазные автотрансформаторы | |||
| TDGC2-0.5 kVa, 2A | АОСН-2-220-82 | ||
| TDGC2-1.0 kVa, 4A | Латр 1.25 | АОСН-4-220-82 | |
| TDGC2-2.0 kVa, 8A | Латр 2.5 | АОСН-8-220-82 | |
| TDGC2-3.0 kVa, 12A | |||
| TDGC2-4.0 kVa, 16A | |||
| TDGC2-5.0 kVa, 20A | АОСН-20-220 | ||
| TDGC2-7.0 kVa, 28A | |||
| TDGC2-10 kVa, 40A | АОМН-40-220 | ||
| TDGC2-15 kVa, 60A | |||
| TDGC2-20 kVa, 80A | |||
https://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
https://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
https://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).
https://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
https://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html (комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ https://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ)
https://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.
Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др.) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
- К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
- К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик). Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ: Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание: Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
- Полное сопротивление (импеданс) Z=R+iX
- Полная мощность S=P+iQ
- Диэлектрическая проницаемость e=e’+ie»
- Магнитная проницаемость m=m’+im»
- и др.
Вопрос 2:
На странице https://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ: Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
Вопрос 3: Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ: Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
См. дополнительную литературу, например:
[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский , 2004.
[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский , 2007.
[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
[4]. AC power, Power factor, Electrical resistance, Reactance https://en.wikipedia.org (перевод: https://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН
Учет реактивной мощности двигателей
Теперь давайте посмотрим, как вычисляется активная энергия для тех же электродвигателей, от которых на 70-80% зависит работоспособность современного предприятия – они крутят насосы, станки, вентиляторы, конвейеры и т.д. и т.п. Раз это так, то кто-то должен постоянно следить за тем, чтобы потребление мощности не стало вдруг необоснованно завышенным. Конечно, осуществлять такой контроль, скорее всего, будет компьютер, но не без участия человека (инженера).
Более всего реактивная энергия мощности тратится попусту в тех случаях, когда двигатель работает на холостых оборотах и если для насосов или конвейеров это ничтожная часть, то для станков – весьма ощутимое разбазаривание реактива. Но, порог наиболее эффективной работы электродвигателей находится в пределах 60-100%, а при более низких показателях бесполезный расход энергии все больше и больше приближается к значению холостого хода. О чем это говорит? О том, что при проектировании цеха не следует завышать его мощности – на практике это пойдёт только во вред производству.
Примечание: мировая практика показывает, что в последнее время инженеры-технологи ведущих предприятий отказываются от фазных роторов и отдают предпочтение асинхронным двигателям с короткозамкнутым ротором.
Понятия активной, полной и реактивной мощностей
Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
| p(t) = u(t) ?i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ) | (5.1) |
и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.
Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):
Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п.
Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.
Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:
| . | (5.2) |
Единица измерения полной мощности S = UI – ВА.
Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – ВАр.
Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.
Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).
Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.
Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВАр на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВАр/км; воздушная линия 220 кВ – 150 кВАр/км; подземный кабель 220 кВ – 3 МВАр/км.
Коэффициент мощности и коэффициент реактивной мощности.
Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.
Рис. 5.1. Треугольник мощностей
Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности.
Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).
Предельные значения коэффициентов реактивной мощности (tgφ) нормируются в зависимости от положения точки (напряжения) присоединения потребителя к сети. Для напряжения сети 100 кВ tgφ = 0,5; для сетей 35, 20, 6 кВ – tgφ = 0,4 и для сети 0,4 кВ – tgφ = 0,35.
Введение новых директивных документов по компенсации реактивной мощности было направлено на повышение эффективности работы всей системы электроснабжения от генераторов энергосистемы до приемников электроэнергии.
С введением коэффициента реактивной мощности стало возможным представлять потери активной мощности через активную или реактивную мощности: Р = (P2/U2) R (l + tg2φ).
Угол между векторами мощностей Р и S соответствует углу φ между векторами активной составляющей тока Iа и полного тока I, который, в свою очередь, представляет собой векторную сумму активного тока Iа, находящегося в фазе с напряжением, и реактивного тока Iр, находящегося под углом 90° к нему. Это расположение токов является расчетным приемом, связанным с разложением на активную и реактивную мощности, которое можно считать естественным.
Большинство потребителей нуждаются в реактивной мощности, поскольку они функционируют благодаря изменению магнитного поля. Для наиболее употребительных двигателей в нормальном режиме работы можно привести следующие примерные значения tgφ.
| Электродвигатели | tgφ | cosφ |
| Однофазный асинхронный двигатель | 1,30–0,90 | 0,61–0,74 |
| Трехфазный асинхронный двигатель | 1,00–0,50 | 0,70–0,89 |
| Коллекторный двигатель | 1,30–1,00 | 0,61–0,70 |
В момент пуска двигателей требуется значительное количество реактивной мощности, при этом tgφ = 4–5 (cosφ = 0,2–0,24).
Синхронные машины обладают способностью потреблять или выдавать реактивную мощность в зависимости от степени возбуждения.
В синхронных генераторах и двигателях размеры цепей возбуждения ограничивают возможность поставки реактивной мощности до максимальных значений tgφ = 0,75 (cosφ = 0,8) или до tgφ = 0,5 (cosφ = 0,9) (табл. 5.1).
Синхронные двигатели, выпускаемые отечественной промышленностью, рассчитаны на опережающий коэффициент мощности (cosφ = 0,9) и при номинальной активной нагрузке Pном и напряжении Uном могут вырабатывать номинальную реактивную мощность Qном ≈ 0,5Pном.
При недогрузке СД по активной мощности β = P/Pном < 1 возможна перегрузка по реактивной мощности α = Q/Qном > 1.
Преимуществом СД, используемым для компенсации реактивной мощности, по сравнению с КБ является возможность плавного регулирования генерируемой реактивной мощности. Недостатком является то, что активные потери на генерирование реактивной мощности для СД больше, чем для КБ.
Дополнительные активные потери в обмотке СД, вызываемые генерируемой реактивной мощностью в пределах изменения cosφ от 1 до 0,9 при номинальной активной мощности СД, равной Pном, кВт:
Рном = Q2номR /U2ном ,
где Qном – номинальная реактивная мощность СД, кВ Ар; R – сопротивление одной фазы обмотки СД в нагретом состоянии, Ом; Uном – номинальное напряжение сети, кВ.
В системах электроснабжения промышленных предприятий КБ компенсируют реактивную мощность базисной (основной) части графиков нагрузок, а СД снижают пики нагрузок графика.
Таблица 5.1
Зависимости коэффициента перегрузки по реактивной мощности синхронных двигателей
| Серия, номинальное напряжение, частота вращения двига теля | Относительное напряжение на зажимах двигателя U/Uном | Коэффициент перегрузки по реактивной мощности α при коэффициенте загрузки β | ||
| 0,90 | 0,80 | 0,70 | ||
| СДН, 6 и 10 кВ (для всех частот вращения) СДН, 6 кВ: 600–1000 об/мин 370–500 об/мин 187–300 об/мин 100–167 об/мин СДН, 10 кВ: 1000 об/мин 250–750 об/мин СТД, 6 и 10 кВ, 3000 об/мин СД и СДЗ, 380 В (для всех частот вращения) | 0,95 1,00 1,05 1,10 1,10 1,10 1,10 1,10 1,10 0,95 1,00 1,05 1,10 0,95 1,00 1,05 1,10 | 1,31 1,21 1,06 0,89 0,88 0,86 0,81 0,90 0,86 1,30 1,32 1,12 0,90 1,16 1,15 1,10 0,90 | 1,39 1,27 1,12 0,94 0,92 0,88 0,85 0,98 0,90 1,42 1,34 1,23 1,08 1,26 1,24 1,18 1,06 | 1,45 1,33 1,17 0,96 0,94 0,90 0,87 1,00 0,92 1,52 1,43 1,31 1,16 1,36 1,32 1,25 1,15 |
Синхронные компенсаторы.
Разновидностью СД являются синхронные компенсаторы (СК), которые представляют собой СД без нагрузки на валу. В настоящее время выпускается СК мощностью выше 5000 кВ?Ар. Они имеют ограниченное применение в сетях промышленных предприятий. Для улучшения показателей качества напряжения у мощных ЭП с резкопеременной, ударной нагрузкой (дуговые печи, прокатные станы и т. п.) используются СК.
Статические тиристорные компенсирующие устройства.
В сетях с резкопеременной ударной нагрузкой на напряжении 6–10 кВ рекомендуется применение не конденсаторных батарей, а специальных быстродействующих источников реактивной мощности (ИРМ), которые должны устанавливаться вблизи таких ЭП. Схема ИРМ приведена на рис. 5.2. В ней в качестве регулируемой индуктивности используются индуктивности LR и нерегулируемые ёмкости С1–С3.
Рис. 5.2. Быстродействующие источники реактивной мощности
Регулирование индуктивности осуществляется тиристорными группами VS, управляющие электроды которых подсоединены к схеме управления. Достоинствами статических ИРМ являются отсутствие вращающихся частей, относительная плавность регулирования реактивной мощности, выдаваемой в сеть, возможность трёх- и четырёхкратной перегрузки по реактивной мощности. К недостаткам относится появление высших гармоник, которые могут возникнуть при глубоком регулировании реактивной мощности.
За счет дополнительных потерь мощности в сети, вызванных потреблением реактивной мощности, увеличивается общее потребление электроэнергии. Поэтому снижение перетоков реактивной мощности является одной из основных задач эксплуатации электрических сетей.
Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
| p(t) = u(t) ?i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ) | (5.1) |
и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.
Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):
Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п.
Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.
Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:
| . | (5.2) |
Единица измерения полной мощности S = UI – ВА.
Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – ВАр.
Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.
Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).
Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.
Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВАр на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВАр/км; воздушная линия 220 кВ – 150 кВАр/км; подземный кабель 220 кВ – 3 МВАр/км.
Коэффициент мощности и коэффициент реактивной мощности.
Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.
Рис. 5.1. Треугольник мощностей
Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности.
Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).
Предельные значения коэффициентов реактивной мощности (tgφ) нормируются в зависимости от положения точки (напряжения) присоединения потребителя к сети. Для напряжения сети 100 кВ tgφ = 0,5; для сетей 35, 20, 6 кВ – tgφ = 0,4 и для сети 0,4 кВ – tgφ = 0,35.
Введение новых директивных документов по компенсации реактивной мощности было направлено на повышение эффективности работы всей системы электроснабжения от генераторов энергосистемы до приемников электроэнергии.
С введением коэффициента реактивной мощности стало возможным представлять потери активной мощности через активную или реактивную мощности: Р = (P2/U2) R (l + tg2φ).
Угол между векторами мощностей Р и S соответствует углу φ между векторами активной составляющей тока Iа и полного тока I, который, в свою очередь, представляет собой векторную сумму активного тока Iа, находящегося в фазе с напряжением, и реактивного тока Iр, находящегося под углом 90° к нему. Это расположение токов является расчетным приемом, связанным с разложением на активную и реактивную мощности, которое можно считать естественным.
Большинство потребителей нуждаются в реактивной мощности, поскольку они функционируют благодаря изменению магнитного поля. Для наиболее употребительных двигателей в нормальном режиме работы можно привести следующие примерные значения tgφ.
| Электродвигатели | tgφ | cosφ |
| Однофазный асинхронный двигатель | 1,30–0,90 | 0,61–0,74 |
| Трехфазный асинхронный двигатель | 1,00–0,50 | 0,70–0,89 |
| Коллекторный двигатель | 1,30–1,00 | 0,61–0,70 |
В момент пуска двигателей требуется значительное количество реактивной мощности, при этом tgφ = 4–5 (cosφ = 0,2–0,24).
Синхронные машины обладают способностью потреблять или выдавать реактивную мощность в зависимости от степени возбуждения.
В синхронных генераторах и двигателях размеры цепей возбуждения ограничивают возможность поставки реактивной мощности до максимальных значений tgφ = 0,75 (cosφ = 0,8) или до tgφ = 0,5 (cosφ = 0,9) (табл. 5.1).
Синхронные двигатели, выпускаемые отечественной промышленностью, рассчитаны на опережающий коэффициент мощности (cosφ = 0,9) и при номинальной активной нагрузке Pном и напряжении Uном могут вырабатывать номинальную реактивную мощность Qном ≈ 0,5Pном.
При недогрузке СД по активной мощности β = P/Pном < 1 возможна перегрузка по реактивной мощности α = Q/Qном > 1.
Преимуществом СД, используемым для компенсации реактивной мощности, по сравнению с КБ является возможность плавного регулирования генерируемой реактивной мощности. Недостатком является то, что активные потери на генерирование реактивной мощности для СД больше, чем для КБ.
Дополнительные активные потери в обмотке СД, вызываемые генерируемой реактивной мощностью в пределах изменения cosφ от 1 до 0,9 при номинальной активной мощности СД, равной Pном, кВт:
Рном = Q2номR /U2ном ,
где Qном – номинальная реактивная мощность СД, кВ Ар; R – сопротивление одной фазы обмотки СД в нагретом состоянии, Ом; Uном – номинальное напряжение сети, кВ.
В системах электроснабжения промышленных предприятий КБ компенсируют реактивную мощность базисной (основной) части графиков нагрузок, а СД снижают пики нагрузок графика.
Таблица 5.1
Зависимости коэффициента перегрузки по реактивной мощности синхронных двигателей
| Серия, номинальное напряжение, частота вращения двига теля | Относительное напряжение на зажимах двигателя U/Uном | Коэффициент перегрузки по реактивной мощности α при коэффициенте загрузки β | ||
| 0,90 | 0,80 | 0,70 | ||
| СДН, 6 и 10 кВ (для всех частот вращения) СДН, 6 кВ: 600–1000 об/мин 370–500 об/мин 187–300 об/мин 100–167 об/мин СДН, 10 кВ: 1000 об/мин 250–750 об/мин СТД, 6 и 10 кВ, 3000 об/мин СД и СДЗ, 380 В (для всех частот вращения) | 0,95 1,00 1,05 1,10 1,10 1,10 1,10 1,10 1,10 0,95 1,00 1,05 1,10 0,95 1,00 1,05 1,10 | 1,31 1,21 1,06 0,89 0,88 0,86 0,81 0,90 0,86 1,30 1,32 1,12 0,90 1,16 1,15 1,10 0,90 | 1,39 1,27 1,12 0,94 0,92 0,88 0,85 0,98 0,90 1,42 1,34 1,23 1,08 1,26 1,24 1,18 1,06 | 1,45 1,33 1,17 0,96 0,94 0,90 0,87 1,00 0,92 1,52 1,43 1,31 1,16 1,36 1,32 1,25 1,15 |
Синхронные компенсаторы.
Разновидностью СД являются синхронные компенсаторы (СК), которые представляют собой СД без нагрузки на валу. В настоящее время выпускается СК мощностью выше 5000 кВ?Ар. Они имеют ограниченное применение в сетях промышленных предприятий. Для улучшения показателей качества напряжения у мощных ЭП с резкопеременной, ударной нагрузкой (дуговые печи, прокатные станы и т. п.) используются СК.
Статические тиристорные компенсирующие устройства.
В сетях с резкопеременной ударной нагрузкой на напряжении 6–10 кВ рекомендуется применение не конденсаторных батарей, а специальных быстродействующих источников реактивной мощности (ИРМ), которые должны устанавливаться вблизи таких ЭП. Схема ИРМ приведена на рис. 5.2. В ней в качестве регулируемой индуктивности используются индуктивности LR и нерегулируемые ёмкости С1–С3.
Рис. 5.2. Быстродействующие источники реактивной мощности
Регулирование индуктивности осуществляется тиристорными группами VS, управляющие электроды которых подсоединены к схеме управления. Достоинствами статических ИРМ являются отсутствие вращающихся частей, относительная плавность регулирования реактивной мощности, выдаваемой в сеть, возможность трёх- и четырёхкратной перегрузки по реактивной мощности. К недостаткам относится появление высших гармоник, которые могут возникнуть при глубоком регулировании реактивной мощности.
За счет дополнительных потерь мощности в сети, вызванных потреблением реактивной мощности, увеличивается общее потребление электроэнергии. Поэтому снижение перетоков реактивной мощности является одной из основных задач эксплуатации электрических сетей.
Возникновение реактивная мощность
Допустим, цепь содержит источник питания постоянного тока и идеальную индуктивность. Включение цепи порождает переходный процесс. Напряжение стремится достичь номинального значения, росту активно мешает собственное потокосцепление индуктивности. Каждый виток провода согнут круговой траекторией. Образуемое магнитное поле будет пересекать соседствующий сегмент. Если витки расположены один за другим, характер взаимодействия усилится. Рассмотренное называется собственным потокосцеплением.
Будет интересно➡ Векторная диаграмма токов и напряжений
Характер процесса таков: наводимая ЭДС препятствует изменениям поля. Ток пытается стремительно вырасти, потокосцепление тянет обратно. Вместо ступеньки видим сглаженный выступ. Энергия магнитного поля потрачена, чтобы воспрепятствовать процессу создавшему. Случай возникновения реактивной мощности. Фазой отличается от полезной, вредит. Идеально: направление вектора перпендикулярно активной составляющей. Подразумевается, сопротивление провода нулевое (фантастический расклад).
При выключении цепи процесс повторится обратным порядком. Ток стремится мгновенно упасть до нуля, в магнитном поле запасена энергия. Пропади индуктивность, переход пройдет внезапно, потокосцепление придает процессу иную окраску:
- Уменьшение тока вызывает снижение напряженности магнитного поля.
- Произведенный эффект наводит противо-ЭДС витков.
- В результате после отключения источника питания ток продолжает существовать, понемногу затухая.
Графики напряжения, тока, мощности
Реактивная мощность некое звено инерции, постоянно запаздывающее, мешающее. Первый вопрос: зачем тогда нужны индуктивности? О, у них хватает полезных качеств. Польза заставляет мириться с реактивной мощностью. Распространенным положительным эффектом назовем работу электрических двигателей. Передача энергии идет через магнитный поток. Меж витками одной катушки, как было показано выше. Взаимодействию подвержены постоянный магнит, дроссель, все, способное захватить вектором индукции.
Случаи нельзя назвать в смысле описательном всеобъемлющими. Иногда применяется поток сцепления в виде, показанном для примера. Принцип используют пускорегулирующие аппараты газоразрядных ламп. Дроссель снабжен несметным количеством витков: отключение напряжения вызывает не плавное снижение тока, но выброс большой амплитуды противоположной полярности. Индуктивность велика: отклик поистине потрясающий. Превышает исходные 230 вольт на порядок. Достаточно, чтобы возникла искра, лампочка зажглась.
Реактивная мощность и конденсаторы
Реактивная мощность запасается энергией магнитного поля индуктивностями. А конденсатор? Выступает источником возникновения реактивной составляющей. Дополним обзор теорией сложения векторов. Поймет рядовой читатель. В физике электрических сетей часто используются колебательные процессы. Всем известные 220 вольт (теперь принятые 230) в розетке частотой 50 Гц. Синусоида, амплитуда которой равна 315 вольт. Анализируя цепи, удобно представить вращающимся по часовой стрелке вектором.
Анализ цепей графическим методом
Упрощается расчет, можно пояснить инженерное представление реактивной мощности. Угол фазы тока считают равным нулю, откладывается вправо по оси абсцисс (см. рис.). Реактивная энергия индуктивности совпадает фазой с напряжением UL, опережает на 90 градусов ток. Идеальный случай. Практикам приходится учитывать сопротивление обмотки. Реактивной на индуктивности будет часть мощности (см. рис.). Угол меж проекциями важен. Величина называется коэффициентом мощности. Что означает на практике? Перед ответом на вопрос рассмотрим понятие треугольника сопротивлений.
Практическое истолкование коэффициента мощности
Многие замечают неувязку в случае практического рассмотрения реактивной мощности. Для снижения коэффициента рекомендуют параллельно обмоткам двигателя включать конденсаторы большого размера. Индуктивное сопротивление уравновешивает емкостное, ток вновь совпадает с напряжением фазой. Сложно понять вот по какой причине:
- Допустим, к источнику переменного напряжения подключили первичную обмотку трансформатора.
- В идеале активное сопротивление равно нулю. Мощность должна быть реактивной. Но это плохо: угол между напряжением и током стремятся сделать нулевым!
Коэффициент мощности
Величина энергии, запасаемой полем, определяется размером индуктивности или емкости. Прочитаете в любом учебнике физики для ВУЗов (Курс физики Жданова и Маранджяна, т. 2, стр. 234), точнее – пропорциональна квадрату величины. Теория реактивной мощности предполагает: некая энергия запасается каждый период паразитной индуктивностью, емкостью, потом уходит во внешнюю цепь. Получается своеобразная циркуляция внутри колебательного контура. Сильно нагреваются соединительные провода, если индуктивность находится слишком далеко от ёмкости.
Но! Колебательный процесс безучастен работе двигателей, трансформаторов. Теория реактивной мощности предполагает: колебания совершает вся энергия. До последней капли. В трансформаторе, двигателе из поля происходит активная “утечка” энергии на совершение работы, наведение тока вторичной обмотки. Энергия циркулировать между источником и потребителем не может.
Реальная цепь процесс согласования отдельных участков затрудняет. Для перестраховки поставщики требуют установить параллельно обмотке двигателя конденсаторы, чтобы энергия циркулировала в локальном сегменте, не выходила наружу, нагревая соединительные провода. Важно избежать перекомпенсации. Если емкость конденсаторов будет слишком велика, батарея станет причиной увеличения коэффициента мощности.
Что касается сдвига фаз, возникает на вторичной обмотке трансформатора подстанции. Роль играет не это. Двигатель работает, часть энергии не преобразована в полезную работу, отражается назад. В результате возникает коэффициент мощности. Участвующая составляющая индуктивности – технологический, конструкционный дефект. Часть, не приносящая пользы. Скомпенсируем, добавляя конденсаторные блоки.
Проверка правильности согласования ведется по факту отсутствия сдвига фаз между напряжением и током работающего электродвигателя. Лишняя энергия циркулирует меж избыточной индуктивностью обмоток, установленным конденсаторным блоком. Достигнута цель мероприятия – избежать нагрева проводников питающей устройство сети.
Будет интересно➡ Явление самоиндукции
Нелинейная нагрузка
Имеет особенность в том, что напряжение и ток не пропорциональны. К нелинейной нагрузке относятся телевизоры, музыкальные центры, настольные электронные часы, компьютеры и его компоненты. Сама нелинейность обусловлена тем, что данное электронное устройство использует импульсные блоки питания. Для подзарядки конденсатора, которые стоят в импульсном блоке питания, достаточно вершины синусоиды.
В остальное время энергию из сети конденсатор не потребляет. В этом случае ток имеет импульсное качество. К чему это все приводит? Это приводит к тому, что синусоида искажается. Но не все электронные устройства работают с искаженной синусоидой. Эта проблема решается за счет применения стабилизаторов двойного преобразования, где сетевое питание преобразуется в постоянное. Затем из постоянного преобразуется в переменное нужной формы и амплитуды.
Понятие реактивной электроэнергии
Этот вид электроэнергии присущ цепям, в составе которых имеются реактивные элементы. Реактивная электроэнергия — это часть полной поступаемой мощности, которая не расходуется на полезную работу.
В электроцепях постоянного тока понятие реактивной мощности отсутствует. В цепях переменного тока реактивная составляющая возникает только в том случае, когда присутствует индуктивная или емкостная нагрузка. В таком случае наблюдается несоответствие фазы тока с фазой напряжения. Данный сдвиг фаз между напряжением и током обозначается символом «φ».
При индуктивной нагрузке в цепи наблюдается отставание фазы, при емкостной – ее опережение. Поэтому потребителю приходит только часть полной мощности, а основные потери происходят из-за бесполезного нагревания устройств и приборов в процессе эксплуатации.
Потери мощности происходят из-за наличия в электрических устройствах индуктивных катушек и конденсаторов. Из-за них в цепи в течение некоторого времени происходит накопление электроэнергии. После этого запасенная энергия поступает обратно в цепь. К приборам, в составе потребляемой мощности которых имеется реактивная составляющая электроэнергии, относятся переносные электроинструменты, электродвигатели и различная бытовая техника. Эта величина рассчитывается с учетом особого коэффициента мощности, который обозначается как cos φ.
Реактивная мощность — еще раз коротко о главном
Все чаще в различных изданиях и СМИ, в рамках информации о реализации Федерального закона от 23 ноября 2009 г. N 261-ФЗ «Об энергосбережении и о повышении энергетической эффективности…» встречается информация о борьбе с реактивной мощностью в сетевых компаниях и на промышленных предприятиях. Что же это за такое зло, что для борьбы с ним сетевыми компаниями тратятся сотни миллионов рублей, разрабатываются специальные долгосрочные целевые программы мероприятий по управлению реактивной мощностью в электрических сетях, ведутся агитации среди крупных потребителей электроэнергии на установку устройств по компенсации реактивной мощности. Так ли она важна и необходима эта компенсация?
Зачастую, многие потребители подсознательно полагают, что генерирующие компании поставляют два типа электрической энергии, так как оплачивают счета за потребленную активную и реактивную мощность, составляющие полной мощности выдаваемой генерирующими подстанциями. Хотя на самом деле понятие реактивной мощности хоть и общепринято и употребляемо, но не совсем корректно, так как физически реактивной мощности (именно в классическом понимании мощности, как отношения работы ко времени) не существует, так как никакой работы она не совершает.
Активная мощность — та часть электрической энергии, которая идет на совершение полезной работы и в процессе потребления преобразуется в другие типы энергии, например тепловую, механическую или световую.
Название реактивная мощность, по аналогии с реактивным сопротивлением, обусловлено способностью индуктивных и емкостных элементов накапливать и отдавать обратно в сеть, запасенную магнитную или электрическую энергию, и проявлять кажущиеся сопротивление только в цепях переменного тока. В то время как активное сопротивление зависит только от конкретного материала проводника.
Согласно общепринятому утверждению, под условным термином «реактивная мощность» понимают вторую составляющую полной мощности в сетях переменного тока, характеризующую интенсивность обмена/циркуляции электрической энергии между источником и подключенной к нему реактивной нагрузки (элементов индуктивности и/или конденсаторов), которая необходима только для расчетов определяющих влияние реактивных элементов на сеть.
Индуктивные (катушки в трансформаторах, дросселях, индукционных печах, двигателях и пр.) и емкостные (конденсаторные батареи) элементы практически не расходуют электроэнергии (без учета магнитного рассеивания и утечек в конденсаторах), хотя она и используется для создания электромагнитных и электрических/электростатических полей, но в процессе разряда возвращается обратно в сеть. Так как энергия циркулирует, то соответственно есть изменения тока и напряжения, которые можно посчитать в виде условной реактивной мощности используемой только для совершения данных преобразований.
Для электрических цепей в зависимости от подключаемого оборудования можно выделить три ситуации:
- если оборудование имеет практически чистую активную (резистивную) нагрузку, например, лампы накаливания, утюги, электроплиты и др. приборы, то протекающий через цепь переменный ток будет синфазен напряжению (см. рис. ниже). Т.е. ток и напряжение будут совпадать по фазе, угол между напряжением и током ϕ=0. Для данного случая мощность является полностью активной и определяется как произведение тока на напряжение. Мощность, переданная источником, полностью тратится на совершение работы.
Рис. Диаграмма напряжения, тока и мощности для активной (резистивной) нагрузки.
- в оборудовании преобладает только индуктивная нагрузка. В данном случае имеется ситуация когда ток отстает от напряжения на уголϕ (см. рис. ниже), это связано со свойственной индуктивности инерционностью, задерживать появление тока. Для идеального случая, когда ϕ = 90° (в некоторой степени подходит для асинхронных двигателей и трансформаторов, работающих на холостом ходу ϕ > 80°), как видно из рисунка, в первой четверти периода происходит потребление энергии для создания магнитного поля, а во второй четверти его обратная генерация в сеть, т.е. происходит обмен мощностью.
Рис. Диаграмма напряжения, тока и мощности для индуктивной нагрузки.
- третья ситуация аналогична предыдущей, но в данном случае для оборудования с только емкостной нагрузкой, проходящий через него ток будет опережать напряжение (см. рис. ниже).
Рис. Диаграмма напряжения, тока и мощности для емкостной нагрузки.
В реальности нагрузка имеет более-менее выраженную индуктивно-емкостную нагрузку (см. рис. ниже), зависящую от параметров самого оборудования. Из-за смещения фаз напряжения и тока уменьшается величина активной мощности, используемой для совершения полезной работы в системах с индуктивной нагрузкой, так как часть электрической энергии (реактивной мощности) будет циркулировать в энергосистеме и тратиться только на создание магнитных полей, не совершая ничего полезного, что в свою очередь приводит к увеличению тока необходимого для полноценной работы оборудования. В то же время, как известно, все проводники обладают активным сопротивлением, и циркуляция больших токов в системе будет приводить к их нагреву (величина нагрева, а соответственно и потерь, как известно, пропорциональна квадрату тока), а соответственно и к потерям электрической энергии.
Рис. Диаграмма напряжения, тока и мощности для индуктивно-емкостной нагрузки.
Для расчетов полной мощности применяется формула,
где, P — активная мощность, определяется по формуле,
Q — реактивная мощность, определяется по формуле,
U — напряжение, I — сила тока, ϕ — угол между напряжением и током.
Как было сказано выше, перетоки реактивной мощности в сети не выполняют полезной работы, при этом загружают источник, силовые линии, и все коммутационное оборудование, установленное между генерирующими станциями и конечными потребителями, а также нагревая кабели и линии высоковольтных передач, снижая тем самым их пропускную способность (с увеличением температуры растет сопротивление проводов) и создавая бесполезное тепло. Зачем же греть окружающую среду и еще платить за это деньги?
Помимо этого снижение пропускной способности и увеличение потерь из-за нагрева проводов ведет к значительным отклонениям напряжения, нормируемым в соответствии с ГОСТ 13109-97, что в конечном итоге негативно сказывается на:
- уменьшение вращающего момента и частоты вращения асинхронных двигателей, что в конечном итоге, при соответствующей нагрузке может привести к его остановке. Одновременно с уменьшением напряжения (снижения реактивной мощности на 2-3 % за каждый процент напряжения) пропорционально вырастит ток двигателя, что может привести к перегреву изоляции обмоток и уменьшения его срока службы.
- уменьшение световой отдачи осветительных приборов, что скажется на производительности труда рабочих. Для люминесцентных ламп снижения/повышения напряжения на 10% приводят к уменьшению их срока службы на 20-25%. Помимо этого, учитывая то, что многие производители компактных люминесцентных ламп не используют в ЭПРА корректоры коэффициента мощности (ККФ), увеличение питающего напряжения ведет к увеличению потребления реактивной мощности. Без ККФ значение коэффициента мощности находиться на уровне 0.5, что делает проблему компенсации также актуальной для индивидуальных потребителей электроэнергии со значительным количеством данных ламп.
- качество работы и длительность эксплуатации различной бытовой электроаппаратуры.
- на качество работы сварочного оборудования, так при отклонениях напряжения до 15%, на машинах для точечной сварки будет гарантированно получаться брак.
- качество и устойчивость работы энергетических систем, возможно появление такой ситуации как «лавина напряжении», обусловленная нарастающим дефицитом реактивной мощности.
Исходя из всего вышесказанного, решение проблем по компенсации реактивной мощности занимают одно из важнейших мест среди мероприятий направленных на повышение эффективности распределения, передачи и потребления электроэнергии. Ведь от их результатов зависит качественное электроснабжение, а также экономия средств по оплате за потребленную электроэнергию (активную и реактивную) и материальных ресурсов. Поэтому в зависимости от конкретной ситуации, все вопросы по компенсации реактивной мощности необходимо решать с учетом современных разработок и решений для данной области.
Основной безразмерной величиной, характеризующей преобладание реактивной составляющей в оборудование, является коэффициент мощности, который численно равен косинусу сдвига тока относительно приложенного к нагрузке напряжения или отношению потребляемой оборудованием активной мощности (Р), к полной (S).
Таким образом, многие предприятия и генерирующие/распределительные сетевые компании стремятся увеличить cos(ϕ) до 1, чтобы в значительной мере снизить величину потребляемой реактивной мощности. Как было приведено выше, в быту и промышленности в основном преобладает оборудование с индуктивным характером нагрузки, с отставанием тока от напряжения, поэтому используя устройства с емкостной нагрузкой, удается уменьшить сдвиг между током и напряжением в фазе, а соответственно добиться cos(ϕ), близкого к единице.
Этого можно достичь с минимальными затратами путем использования компенсирующих установок построенных на базе конденсаторов (конденсаторные установки КРМ, АУКРМ, батареи статических конденсаторов), более дорогих синхронных двигателей в режиме перевозбуждения или тиристорных схем с фильтрами, устанавливаемых непосредственно вблизи оборудования с преобладающей реактивной нагрузкой или группами, на распределительных подстанциях предприятия. Так создание электрической энергии с преобладающей емкостной характеристикой с генерирующих синхронными генераторами подстанций, в целом не целесообразно, ввиду тех же самых потерь при передаче и распределении электрической энергии.
В последнее время все более востребованными становятся конденсаторные установки АУКРМ, позволяющие производить более точную коррекцию коэффициента мощности с учетом изменения значений, потребляемой мощности от токов нагрузки, напряжения, времени суток.
При этом при формировании конденсаторной установки желательно обеспечивать максимально малый шаг регулирования, но с использованием минимального количества конденсаторов. В конечном итоге грамотный выбор определенного оборудования для компенсации реактивной мощности определяется на основании технико-экономических расчетов, характера преобладающей в сетях предприятия реактивной нагрузки, что позволит достигнуть положительного экономического эффекта при минимальных сроках окупаемости внедренного оборудования.
По материалам
Расчет реактивной электроэнергии
Коэффициент мощности лежит в пределах от 0,5 до 0,9; точное значение этого параметра можно узнать из паспорта электроприбора. Полная мощность должна быть определена как частное от деления активной мощности на коэффициент.
Например, если в паспорте электрической дрели указана мощность в 600 Вт и значение 0,6, тогда потребляемая устройством полная мощность будет равна 600/06, то есть 1000 ВА. При отсутствии паспортов для вычисления полной мощности прибора коэффициент можно брать равным 0,7.
Поскольку одной из основных задач действующих систем электроснабжения является доставка полезной мощности конечному потребителю, реактивные потери электроэнергии считаются негативным фактором, и возрастание этого показателя ставит под сомнение эффективность электроцепи в целом. Баланс активной и реактивной мощности в цепи может быть наглядно представлен в виде этого забавного рисунка:
Измерение мощности
Измерение активной мощности в сетях производится с помощью ваттметра
Цифровой ваттметр Аналоговый ваттметр
В зависимости от схемы соединения нагрузки и его характера (симметричная или несимметричная) схемы подключения приборов могут разниться. Рассмотрим случай с симметричной нагрузкой:
Схема включения ваттметра при симметричной нагрузке
Здесь измерение проводится всего лишь в одной фазе и далее согласно формуле умножается на три. Этот способ позволяет сэкономить на приборах и уменьшить габариты измерительной установки. Применяется, когда не нужна большая точность измерения в каждой фазе.
Измерение при несимметричной нагрузке:
Схема включения ваттметра при несимметричной нагрузке
Этот способ более точный, так как позволяет измерить мощность каждой фазы, но это требует трех приборов, больших габаритных размеров установки и обработки показаний с трех приборов.
Измерении в цепи без нулевого проводника:
Схема включения ваттметра при отсутствии нулевого провода
Эта схема требует двух приборов. Этот способ основывается на первом законе Кирхгофа
IA+IB+IC=0. Из этого следует, что сумма показаний двух ваттметров равна трехфазной мощности этой цепи. Ниже показана векторная диаграмма для данного случая:
Векторная диаграмма включения двух ваттметров при различных видах нагрузки
Мы можем сделать вывод, что показания приборов зависят не только от величины, но еще и от характера нагрузки.
Из диаграммы следует, что мы можем определить показание приборов аналитически:
Проанализировав полученный результат можем сделать вывод что, при преобладании активной нагрузки (φ=0) результаты измерения ваттметров тождественны (W1=W2). При активной и индуктивной (R-L) показания W1 меньше чем W2 (W12), при φ>600 показания W1 вообще отрицательные (W1<0).
При активной и емкостной(R-C) и W1>W2, а при φ<-600 показания W2 <0.
При современном развитии техники появились цифровые ваттметры. Они в отличии от аналоговых меньше в размерах, гораздо легче и менее габаритны. Более того цифровые ваттметры могут фиксировать ток, напряжение, измерять cosφ в сети и другое. Они позволяют в режиме реального времени отслеживать различные величины и выдавать предупреждения при их отклонении. Это очень удобно и не требуется проводить измерения тока, напряжения, а потом математически это все высчитывать. Цифровой ваттметр заключен в корпус и подключается (для бытовых потребителей) самым обычным способом – как и обычный потребитель — втыканием вилки в розетку.
Различия
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Вам это будет интересно Особенности единиц измерения кВТ и кВА
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания.
Смысл реактивной нагрузки
Любая реактивная нагрузка создает временной сдвиг между фазами тока и напряжения. Эту величину измеряют в градусах. Наиболее наглядным является векторное представление электрических параметров. Если подключить индуктивность, напряжение будет опережать ток. Угол между ними обозначают в формулах буквой «ϕ» («Фи» греч.).
Временные и векторные диаграммы показывают, как изменяются основные параметры при подключении индуктивных (емкостных) элементов
На картинке показано, что при подключении емкостной нагрузки вектора «меняются» местами. В идеальных условиях сдвиг между векторами равен 90°. В действительности следует учитывать влияние электрического сопротивления цепи, несовершенство конструкций. С учетом особенностей элементов следует напомнить, что в индуктивности (емкости) при сохранении параметров источника питания плавно изменяется ток (напряжение), соответственно.
Почему в сети напряжение переменное
Для объяснения настоящей ситуации надо сделать краткий экскурс в историю. Электричество известно человеку сотни (по некоторым данным, тысячи лет). Однако действительно массовое использование этой энергии началось сравнительно недавно – в конце 19 века. Именно тогда (1879 г.) Эдисон запатентовал первый функциональный прибор, который помогал решать проблемы освещения. Для питания лампочек он стал монтировать сети постоянного тока.
Через десять лет Тесла создал генераторы переменного тока. После ожесточенной конкурентной борьбы именно его способ передачи энергии на расстояния одержал победу. Этот результат был обеспечен скорее рыночными методами, чем внимательным сравнением потребительских характеристик.
Расчёт мощности по току и напряжению
Формула мощности электрического тока
Посчитать потребление P можно, зная эти два параметра I и U сети. До того, как подобрать кабели или провода для проводки в квартире, нужно определиться с P потребителей, которые можно к ним подключить. Расчёт производят после того, как измерительными приборами фиксируют действующие показания силы тока I (А), а также напряжения U (В).
Однофазная сеть напряжением 220 вольт
При включении в цепь активной нагрузки пользуются формулой: P = U*I. В случае присутствия сдвига фаз между U и I пользуются формулой: P = U*I* cosφ.
Трёхфазная сеть напряжением 380 В
В трёхфазной сети переменного тока со сдвигом фаз результат последней формулы умножают на √3. Значение угла cosφ можно уточнить в справочнике.
Таблица cosφ для бытовых устройств
При выборе сечения проводов обычно известны суммарная мощность будущих потребителей и напряжение сети.
Нужна только сила тока формула через мощность и напряжение которой имеет вид:
I = P / (U *cosφ).
У формулы для расчёта тока, используя мощность и напряжение, следующие составляющие:
- P – известная мощность прибора, (Вт);
- U – напряжение питания, (220/380 В);
- cosφ – угол сдвига фаз.
Расчет тока можно выполнить с помощью онлайн-калькулятора.
Онлайн-калькулятор – общий вид интерфейса