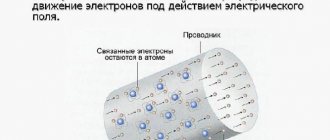
Почему возникает сопротивление
Электроны, сталкиваясь с заряженными атомами (ионами), из которых стоит кристаллическая решетка проводника, теряют скорость. Масса атома значительно превосходит массу электрона, поэтому их столкновение приводит к потере скорости (“торможению”) и изменению направления движения электрона. Таким образом возникает сопротивление протеканию (нарастанию) тока. Значит сопротивление — это физическая величина.
Столкновения электронов с атомами.
В чем измеряется
Согласно международной системе единиц, измеряется величина в омах, умноженных на метр. В некоторых случаях применяется единица ом, умноженная на миллиметр в квадрате, поделенная на метр. Это обозначение для проводника, имеющего метровую длину и миллиметровую площадь сечения в квадрате.
Единица измерения
Что такое электрическое сопротивление
Позиционируется как сопротивление некоторого элемента, служащего проводником. Он имеет единичную длину, показатель площади сечения. В этом заключается физический смысл. Электрическое сопротивление – это параметр проводника, опирающийся на зависимость от:
- структуры материала;
- параметра формы;
- габаритов изделия.
Формула как найти
Согласно положению из любого учебного пособия по электродинамики, удельное сопротивление материала проводника формула равна пропорции общего сопротивления проводника на площадь поперечного сечения, поделенного на проводниковую длину. Важно понимать, что на конечный показатель будет влиять температура и степень материальной чистоты. К примеру, если в медь добавить немного марганца, то общий показатель будет увеличен в несколько раз.
Главная формула расчета
Интересно, что существует формула для неоднородного изотропного материала. Для этого нужно знать напряженность электрополя с плотностью электротока. Для нахождения нужно поделить первую величину на другую. В данном случае получится не константа, а скалярная величина.
Закон ома в дифференциальной форме
Есть другая, более сложная для понимания формула для неоднородного анизотропного материала. Зависит от тензорного координата.
Важно отметить, что связь сопротивления с проводимостью также выражается формулами. Существуют правила для нахождения изотропных и анизотропных материалов через тензорные компоненты. Они показаны ниже в схеме.
Связь с проводимостью, выраженная в физических соотношениях
Пример задачи №1
Длина медного провода, использованного в осветительной сети, $100 \space м$, площадь поперечного сечения его $2 \space мм^2$. Чему равно сопротивление такого провода?
Для того, чтобы рассчитать сопротивление такого проводника, нам понадобится значение его удельного сопротивления. Удельное сопротивление меди равно $0.017 \frac{Ом \cdot мм^2}{м}$. Так как эта величина нам дана именно в этих единицах измерения, мы не будем переводить в СИ значение площади поперечного сечения, выраженное в $мм^2$.
Теперь мы можем записать условие задачи и решить ее.
Дано: $l = 100 \space м$ $S = 2 \space мм^2$ $\rho = 0.017 \frac{Ом \cdot мм^2}{м}$
$R — ?$
Решение:
Формула для расчета сопротивления проводника: $R = \frac{\rho l}{S}$.
Рассчитаем его: $R = \frac{0.017 \frac{Ом \cdot мм^2}{м} \cdot 100 \space м}{2 \space мм^2} = \frac{1.7 \space Ом}{2} = 0.85 \space Ом$.
Ответ: $R = 0.85 \space Ом$.
От чего зависит
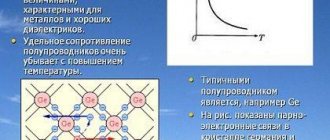
Сопротивляемость зависит от температуры. Она увеличивается, когда повышается столбик термометра. Это поясняется физиками так, что при росте температуры атомные колебания в кристаллической проводниковой решетке повышаются. Это препятствует тому, чтобы свободные электроны двигались.
Обратите внимание! Что касается полупроводников и диэлектриков, то там величина понижается из-за того, что увеличивается структура концентрации зарядных носителей.
Зависимость от температуры как основное свойство проводниковой сопротивляемости
Что означают показатели удельного сопротивления?
Для того чтобы иметь возможность сравнивать удельное сопротивление различных материалов, от таких изделий, как медь и алюминий, до других металлов и веществ, включая висмут, латунь и даже полупроводники, необходимо использовать стандартное измерение.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м.
Единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м2, изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2
Значения удельных сопротивлений некоторых веществ
В таблице 1 приведены значения удельных сопротивлений некоторых веществ.
| Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ | Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ |
| Серебро | $0.016$ | Манганин (сплав) | $0.43$ |
| Медь | $0.017$ | Константан (сплав) | $0.50$ |
| Золото | $0.024$ | Ртуть | $0.96$ |
| Алюминий | $0.028$ | Нихром (сплав) | $1.1$ |
| Вольфрам | $0.055$ | Фехраль (сплав) | $1.3$ |
| Железо | $0.10$ | Графит | $13$ |
| Свинец | $0.21$ | Фарфор | $10^{19}$ |
| Никелин (сплав) | $0.40$ | Эбонит | $10^{20}$ |
Таблица 1. Удельное сопротивление некоторых веществ (при $t = 20 \space \degree C$)
Обратите внимание, что эти значения актуальны при температуре $20 \space \degree C$.
Удельное сопротивление вещества зависит от температуры.
Опыты показали, что при определенной температуре для каждого вещества диэлектрик может стать проводником (полупроводник). Также экспериментально доказано, что с повышением температуры удельное сопротивление металлов увеличивается.
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких «популярных» материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
МатериалУдельное сопротивление, ρ,при 20 °C (Ом·м)Источник
| Латунь | ~0.6 — 0.9 x 10-7 | |
| Серебро | 1.59×10−8 | [3][4] |
| Медь | 1.68×10−8 | [5][6] |
| Обожжённая медь | 1.72×10−8 | [7] |
| Золото | 2.44×10−8 | [3] |
| Алюминий | 2.65×10−8 | [3] |
| Кальций | 3.36×10−8 | |
| Вольфрам | 5.60×10−8 | [3] |
| Цинк | 5.90×10−8 | |
| Кобальт | 6.24×10−8 | |
| Никель | 6.99×10−8 | |
| Рутений | 7.10×10−8 | |
| Литий | 9.28×10−8 | |
| Железо | 9.70×10−8 | [3] |
| Платина | 1.06×10−7 | [3] |
| Олово | 1.09×10−7 | |
| Тантал | 1.3×10−7 | |
| Галлий | 1.40×10−7 | |
| Ниобий | 1.40×10−7 | [8] |
| Углеродистая сталь (1010) | 1.43×10−7 | [9] |
| Свинец | 2.20×10−7 | [2][3] |
| Галинстан | 2.89×10−7 | [10] |
| Титан | 4.20×10−7 | |
| Электротехническая сталь | 4.60×10−7 | [11] |
| Манганин (сплав) | 4.82×10−7 | [2] |
| Константан (сплав) | 4.90×10−7 | [2] |
| Нержавеющая сталь | 6.90×10−7 | |
| Ртуть | 9.80×10−7 | [2] |
| Марганец | 1.44×10−6 | |
| Нихром (сплав) | 1.10×10−6 | [2][3] |
| Углерод (аморфный) | 5×10−4 — 8×10−4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 — 5.0×10−6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 | |
| Арсенид галлия | 10−3 to 108 | |
| Германий | 4.6×10−1 | [3][4] |
| Морская вода | 2.1×10−1 | |
| Вода в плавательном бассейне | 3.3×10−1 — 4.0×10−1 | |
| Питьевая вода | 2×101 — 2×103 | |
| Кремний | 2.3×103 | [2][3] |
| Древесина (влажная) | 103 — 104 | |
| Деионизированная вода | 1.8×105 | |
| Стекло | 1011 — 1015 | [3][4] |
| Углерод (алмаз) | 1012 | |
| Твердая резина | 1013 | [3] |
| Воздух | 109 — 1015 | |
| Древесина (сухая) | 1014 — 1016 | |
| Сера | 1015 | [3] |
| Плавленый кварц | 7.5×1017 | [3] |
| ПЭТ | 1021 | |
| Тефлон | 1023 — 1025 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Будет интересно➡ Тепловое реле для электродвигателя
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах — никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Понятие электрического сопротивления проводника
Классическое определение объясняет электрический ток движением «свободных» (валентных) электронов. Его обеспечивает созданное источником электрическое поле. Перемещение в металле затрудняют не только нормальные компоненты кристаллической решетки, но и дефектные участки, примеси, неоднородные области. В ходе столкновений с препятствиями за счет перехода импульса в тепловую энергию происходит повышение температуры.
Наглядный пример – нагрев воды кипятильником
В газах, электролитах и других материалах несколько отличная физика явления. Линейные зависимости наблюдаются в металлах и других проводниках. Базовые соотношения выражены известной формулой закона Ома:
R (электрическое сопротивление) = U (напряжение)/ I (сила тока).
Для удобства часто используют обратную величину, проводимость (G = 1/R). Она обозначает способность определенного материала пропускать ток с определенными потерями.
Для упрощения иногда применяют пример с водопроводом. Движущаяся жидкость – аналог тока. Давление – эквивалент напряжения. Уменьшением (увеличением) поперечного сечения или положением запорного устройства определяют условия перемещения. Подобным образом изменяют основные параметры электрических цепей с помощью сопротивления (R).
К сведению. Количество жидкости, проходящее за единицу времени через контрольное сечение трубы, – эквивалент электрической мощности.
Формулировка закона Ома
Сила тока на конкретном участке цепи будет прямо пропорциональной напряжению и обратно пропорциональной сопротивлению.
Закон Ома для участка цепи
Приведён по классической формуле: \( I=U/R \)
Здесь не учитывается сопротивление всей цепи, но допускается возможность измерить показатель сопротивления на каждом отдельном участке.
Закон Ома для полной цепи
Определяется формулой:
\[ I= E/R+r \]
Как определение, данная формулировка будет звучать как: сила тока прямо пропорциональна ЭДС и обратно пропорциональна общему сопротивлению. Под общим сопротивлением подразумевается сумма внешнего и внутреннего сопротивлений.
Закон Ома в дифференциальной и интегральной формах
- В дифференциальной форме применяется при необходимости определить параметры ничтожно малого участка цепи.
- В интегральной форме рассматривается цепь, с расчётом на наличие источника тока, а также без него.
Температурная зависимость ρ(Т)
Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.
Удельное сопротивление металлов и сплавов, Ом*мм2/м
(при Т = 20С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (6),
где: ρ — удельное сопротивление проводника при температуре 0С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность или .
В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.
2021 г. Справочники – Мобильная версия — Электротехника
• Электрические предохранители. • Современные магниты (определение полярности, измерение индукции). • Источники Бесперебойного Питания (ИБП) • Солнечные батареи и термогенераторы (автономное электропитание). • Таблица удельных электросопротивлений (для металлов, графита, воды и земли). • «Земляная электрическая батарея» – свободная энергия (СЕ). • Аккумуляторы различных типоразмеров – как выбрать и протестировать.
Памятка по электротехнике
Закон Ома устанавливает связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах. Формулировка для участка электрической цепи (проводника), не содержащего источников электродвижущей силы (ЭДС): сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. Законы Ома для замкнутой неразветвлённой цепи: сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению цепи. Закон Ома справедлив для постоянных и квазистационарных токов. Был открыт немецким физиком Георгом Омом в 1826 году. * Современная энциклопедия
В случае переменного тока, величины, входящие в расчётные формулы – становятся комплексными.
Закон Ома в дифференциальной форме – описывает исключительно электропроводящие свойства материала, вне зависимости от геометрических размеров.
Удельное электрическое сопротивление вещества есть электросопротивление изготовленного из него куба со сторонами, равными единице (1метр), когда ток идёт перпендикулярно двум его противоположным граням, площадью 1 квадратный метр каждая.
Удельное сопротивление зависит от концентрации в проводнике свободных электронов и от расстояния между ионами кристаллической решетки, иначе говоря, от материала проводника.
Размерность удельного электросопротивления в сист. СИ (международная система единиц, англ. – International System of Units) – Ом·м [Ом*м^2/м]
(SI – Ω·m, рус. – Ом-метр, англ. – ohm-meter). Для измерения проводниковых материалов разрешается использовать внесистемную единицу –
Ом·мм2/м
(для миллиметрового сечения проводника, длиной 1 м., то есть – миллионную часть Ом-метра).
Физический смысл удельного сопротивления: материал (однородный и изотропный*) имеет удельное электрическое сопротивление один Ом·м, если изготовленный из этого материала куб со стороной 1 метр имеет сопротивление 1 Ом при измерении на противоположных гранях куба. * Изотропность – идентичность физических свойств во всех направлениях.
Удельное сопротивление характеризует способность вещества проводить электрический ток и не зависит от формы и размеров вещества, но меняется, при отличии его температуры от 20 °C (то есть, от комнатной, при которой определялись табличные значения для справочников).
На практике, в технике чаще применяется единица, в миллион раз меньшая (миллиметровое токоведущее сечение), чем Ом·м:
1 мкОм·м (SI – µΩ·m, рус. – микроом-метр, англ. – microhm-meter) = 1*10^-6 Ом*м 1 мкОм·м = 1 Ом·мм2/м
При этом, удельное сопротивление однородного куска проводника длиной 1 метр и площадью токоведущего сечения 1 квадратный миллиметр – равно 1 Ом·мм2/м, если его сополтивление равно 1 Ом. Например, величина удельного сопротивления электротехнической меди, примерно, составляет 1,72*10^-8 Ом·м = 0.0172 мкОм·м (определяется при температуре 20 градусов по Цельсию).
В зависимости от удельного сопротивления все вещества делятся на проводники, диэлектрики и полупроводники. Диэлектрики (изоляторы, например – фарфор) имеют очень высокие значения удельного электрического сопротивления, превышающие 10^12 Ом·м, а проводники (к примеру – серебро, медь) – меньше 10^-2 Ом·м (
Соотношения:
1 Ом·мм2/м = 1 мкОм·м ( 1*10^-6 Ом*м ) 1 Ом·см = 0.01 Ом·м 1 Ом·м = 100 Ом·см (ом-сантиметр, англ. Ohm-centimeter)
Электрическая проводимость – это величина, обратная электрическому сопротивлению. В СИ единицей электрической проводимости является Сименс (обозначается – См, анг. – S). Например, медь имеет эл.проводность, приблизительно, равную 58 100 000 См/м ( 1 / 58100000 ~ 0,0172 х 10-6 Ом.м), измеряемую при температуре 20 °C
Формула для расчёта электрического сопротивления при постоянном токе
R = (p * L) / S
где: R – электросопротивление провода; p – удельное сопротивление: p [Ом·мм2/м] = (R * S) / L [ Om * mm^2 / m ] L – длина, м; S – поперечное сечение: квадратный метр или миллиметр (м2 или мм2). S = 3.14 * (радиус)^2
Если удельное эл.сопротивление – в Ом·мм2/м, то S (сечение) – должно быть в мм2, L (длина) – в метрах. Если в Ом·см (Ом-сантиметр, сокращением, из Ом*см^2 / см ), то S в см2, L – в сантиметрах. Если уд.сопр – в Om·m (Ом-метр, из Ом*м^2 / м ), то S в м2, L – в метрах.
1 Ом·мм2/м = 1 мкОм·м (производная дольная единица удельного электрического сопротивления в системе СИ, применяемая, на практике, в технических расчётах – миллионная часть Ом•м)
Для электрика и опытного радиолюбителя, способность на глазок оценить сечение электрического провода, с учётом слоя изоляции – это как абсолютный слух у музыканта, слёту определяющего высоту тона услышанных звуков и записывающего их в виде нотных знаков и ключей регистра.
Пример, в качестве образца по соотношению величин. Удельное электросопротивление чистой электротехнической меди (после её обработки рекристаллизационным отжигом), измеренное при температуре 20 °C:
0,0172 мкОм (микроом-метр, 10^-6 Ом•м)
1.72*10^-2 Ом*мм^2/м (фактическое электр-е сопротивление медного проводника, длиной 1 метр и сечением 1 мм2)
1.72*10^-6 Ом•см (размеры провода – в сантиметрах)
1.72*10^-8 Ом•м (сокращением, из Ом*м^2/м – метровый кубик, площадь токоведущего сечения – 1м2 , т.е. между противоположными гранями)
17.2 нОм•м (наноом-метр, 10^-9 Ом•м)
Металлы высокой проводимости (не более 0,1 мкОм.м) – используются для изготовления проводов, токопроводящих жил кабелей, обмоток электрических машин и трансформаторов и т.п. Металлы и сплавы высокого сопротивления (не менее 0,3 микроом-метр) – применяются для производства образцовых резисторов, реостатов, электроизмерительных приборов, электронагревательных устройств, нитей ламп накаливания и т.п. Нагревательные сплавы должны выдерживать длительную работу на открытом воздухе, без разрушения при температурах не менее 1000 °С.
Таблица значений удельного электрического сопротивления, мкОм·м (микроом-метр) = Ом·мм2/м (равные числовые величины) при температуре окружающей среды 20 градусов по Цельсию Серебро – 0,015-0,016 Медь – 0,0172-0,0180 Золото – 0,024 Алюминий – 0.026-0.030 Вольфрам – 0,053-0,055 Цинк 0,053-0,062 Никель – 0.068-0,073 Латунь (сплав меди с цинком) – 0,043-0,108 Железо – 0,098 Сталь – 0,10-0,14 Олово – 0,12 Оловяно-свинцовый припой – 0,14-0,16 Бронзовые сплавы – 0,02-0,2 Свинец – 0,217-0,227 Никелин – 0,4 Манганин – 0,42-0,48 Константан – 0,48-0,52 Нихром – 1,05-1,40 Фехраль – 1,15-1,35 Угольно-графитовые щётки для электрических машин – 20-50 Угольный сварочный электрод – 50-90 мкОм·м
Минералка (с минерализацией воды – 2-7 грамм на литр) – 1-4 *10^6 мкОм·м = 1-4 Ом•м Вода грунтовая – 10-50 *10^6 Влажная / сырая садовая земля (верхний слой почвы, грунта – после поливки) – 20-60 *10^6
Почему в электросетях применяется высокое напряжение
В линии электропередачи, при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, считается желательным, увеличение напряжения до величин в десятки (внутригородские воздушные и кабельные сети электропередач на 380 вольт, 6, 10, 20, 35, 110, 220 и 330 кВ) и сотни киловольт (магистральные электросети сверхвысокого – ЛЭП500-750 кВ и ультравысокого напряжения, 1150кВ и выше) на линиях переменного и постоянного (150, 400, 800 кВ) тока. Но, при таких параметрах эксплуатации, постоянно растущем потреблении электрической энергии и частых пиковых перегрузках, износ оборудования, отсутствие резервных мощностей, погодные аномалии, локальные несоответствия требованиям безопасности, непрофессионализм и элементарное разгильдяйство – могут стать причиной нештатных ситуаций и системных аварий (называемых теперь, на английский манер – блэкаут). По этой причине, муниципальные власти любого посёлка и города – имеют постоянную головную боль по обеспечению резервными источниками питания (аккумуляторами и дизель-генераторами) для бесперебойного электроснабжения социальных объектов по резервной схеме.
Спецсплавы на медной основе, в электротехнике
При больших токах, до 10 А – применяют проволочный резистор большой мощности, называемый реостатом. В качестве обмотки используют проволоку, изготовленную из термостабильного (с минимальным температурным коэффициентом) сплава с большим удельным сопротивлением, например, из константана (40% Ni, 1,2% Mn, 58,8% Cu). Если напряжение между соседними витками не превышает 1 вольта – такую проволку можно наматывать плотно, виток к витку, без особой изоляции между витками, благодаря наличию естественной плёнки окисла, образующейся на поверхности данного металла, при быстром (не более трёх секунд) нагреве до достаточно высокой температуры (порядка 900 °С).
В приборах высокого класса точности – применяется манганин (3%Ni, 12%Mn, 85%Cu), менее термоустойчивый, но, в отличие от константанового провода, имеющий очень малую термоЭДС (контактную разность электрических потенциалов) в паре с медью.
Обозначения рекомендуемых кратных и дольных величин от единиц СИ
10^9 Ом – гигаом ГОм GΩ 10^6 Ом – мегаом МОм MΩ 10^3 Ом = 1000 Ом – килоом кОм kΩ. 10^-2 Ом – сантиом сОм cΩ 10^-3 Ом – миллиом мОм mΩ. 10^-6 Ом – микроом мкОм µΩ 10^-9 Ом – наноом нОм nΩ
Зависимость сопротивления от температуры
При нагревании, электрическое сопротивление металлических проводников – возрастает, а при охлаждении – уменьшается. Для вычисления, по формуле, электросопротивления при определённой температуре – используют, так называемый, «температурный коэффициент сопротивления» (ТКС). Расчёты ведутся от некоторого начального уровня температуры. Для интервала температур, в пределах обычных погодных условий (в зимнее и летнее время года) окружающей среды, зависимость для проводника описывается математической формулой:
R2 = R1 * (1 + α * (t2 – t1)),
где R1 (начальное, известное значение, при нуле или 20 градусов по Цельсию, измеренное или посчитанное) и R2 (искомое) – сопротивления резистора соответственно при температурах t1 (0°С или 20°С) и t2; α – температурный коэффициент сопротивления (из справочной таблицы), равный относительному изменению электр. сопротивления (удельного или абсолютного) при изменении температуры на 1 °С. Так как значения ТКС очень малы, то в справочниках их указывают в единицах тысячных или миллионных долей (ppm/°С – Parts Per Million) относительного изменения сопротивления на градус.
Обычно, исходные, табличные значения различных физических постоянных – приводятся или к нормальной комнатной температуре +20 °С или к нулевой (в справочных таблицах проводниковых и реостатных материалов, применяемых в электрических аппаратах).
В металлических термометрах, изготавливаемых из медной или платиновой проволоки – электросопротивление, с повышением температуры (без экстремально высоких, для этих материалов, значений) увеличивается почти линейно. Но, при чрезмерно сильном нагреве, к примеру, тонкого медного провода до температуры красного каления, его активное электрическое сопротивление постоянному току возрастает многократно.
Пример расчёта для стометрового алюминиевого шинопровода, радиусом 40 мм, нагретого на 95°С: R = (R1 * (1 + α * (t2–t1))) * L / S = = 2,62*10-8 Ом•м * (1 + 0,0042*95) * 100 / (3,14 * 402 * 10-6) = 7,3 * 10-4 Ом где: S – площадь сечения в м2 (с вычетом толщины слоёв изоляции), L – длина проводника в метрах.
Температурный коэффициент сопротивления х10-3, 1/градус: Алюминий – 4,2 Бронза оловянистая твёрдотянутая – 0,6-0,7 Вольфрам – 4,2 Графит – -1,3 Дюраль – 2,2 Константан – 0,003-0,005 Латунь – 1,5 Манганин – 0,03-0,06 (при температуре до 250-300°С) Медь – 4,3 Нихром – 0,14 Серебро – 4,0 Сталь – 9,0 Цинк – 4,2
Постоянные резисторы и их маркировка
В буквенно-цифровой (кодовой) маркировке резисторов – на их корпус наносится числовое значение электрического сопротивления и буквы, первая из которых обозначает множитель (R или Е – Ом, K – килоом, M – мегаом) и, заодно, определяет положение разделительной запятой десятичного знака. Вторая буква означает класс точности, то есть, допускаемое отклонение от указанной величины. Номиналы на мелкие детали – наносят в виде маркировки цветными кольцами, полосками или точками (в зависимости от применяемого стандарта). Каждому цвету соответствует определенная цифра, означающая число Ом, множитель / степень или процент точности. Для быстрого определения номинала резистора по цветовой кодировке, применяются специальные компьютерные программы. Читать дальше…
Пример расчёта, на основе школьной задачки по физике из программы 9 класса.
Задание: определить (найти в таблице), по известному удельному сопротивлению p = 0.017Ом·мм2/м – какой это материал? Рассчитать диаметр проволоки. Вычислить электрическое сопротивление провода, длиной L = 80 см, сечением S = 0.2 мм2 Решение задачи: По таблице определяем, что удельное сопротивление, равное 0.017 Ом·мм2/м может быть у меди.
Из формулы S = 3.1416 * (радиус)^2 = 3.142 * ((диаметр)^2)/4 с помощью своего калькулятора, находится диаметр (в миллиметрах) = корень квадратный из (4 * S / 3.14)
Длина провода, в единицах системы СИ (переводим в метры): 80 см = 0.8 м
Находим электр. сопротивление по формуле: R = (p * L) / S = (0.017 * 0.8) / 0.2 = 0.068 Ом
Ответ: с точностью до второго знака после запятой, R = 0.07 Ом
[ на главную страницу ]
Р а з м е с т и т ь о б ъ я в л е н и е
Самые свежие Новости финансов от сайта Финверсия.ру Электромонтажные работы – монтаж электрики, подключение и обслуживание электропроводки. | Минисправочник по электрическим параметрам: соотношения Ом х мм2/м и мкОм x м (микроом), в технических расчётах для металлов, сплавов и порошковых смесей.
Copyright © 2007-2021, KAKRAS.RU
Удельное электрическое сопротивление
Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.
Эта функциональная связь хорошо описывается следующей формулой:
$ R = ρ *{ Lover S} $ (4)
Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества. Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:
$ ρ = R*{ Sover L } $ (5)
Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 20С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается. При приближении к температуре абсолютного нуля, которая равна -273С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.
Содержание
Сила тока в цепи определяется электрическим зарядом, проходящим через поперечное сечение проводника за единицу времени: $I = \frac{q}{t}$.
Электрическое напряжение — это еще одна физическая величина, характеризующая электрическое поле. Она равна отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку: $U = \frac{A}{q}$.
Электрическое сопротивление — величина, зависящая от свойств проводника. На значение сопротивления не влияет ни значение силы тока в проводнике, ни значение напряжения на его концах. Его можно рассчитать по формуле $R = \frac{\rho l}{S}$, где $\rho$ — удельное сопротивление проводника, $l$ — длина проводника, $S$ — площадь его поперечного сечения. Значение удельного сопротивления для определенного вещества можно посмотреть в таблице 1 в уроке «Расчет сопротивления проводника. Удельное сопротивление».
Эти три физические величины (силу тока, напряжение и сопротивление) связывает между собой закон Ома для участка цепи: $I = \frac{U}{R}$. Сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
В данном уроке вы научитесь использовать эти знания для решения задач. Мы рассмотрим несколько примеров, а затем перейдем к упражнениям и их подробным решениям.
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
, где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
, будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Итак,
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10-6. Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм2.
- Медь
- Вольфрам
- Никелин
- Железо
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Будет интересно➡ Закон полного тока для магнитного поля
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Упражнения
Упражнение №1
Длина одного провода $20 \space см$, другого — $1.6 \space м$. Площадь сечения и материал проводов одинаковы. У какого провода сопротивление больше и во сколько раз?
Обратите внимание, что если материал проводников один и тот же, то одинаковы и значения удельных сопротивлений $\rho$ для этих проводников.
Дано: $l_1 = 20 \space см$ $l_2 = 1.6 \space м$ $S_1 = S_2 = S$ $\rho_1 = \rho_2 = \rho$
СИ: $l_1 = 0.2 \space м$
$\frac{R_2}{R_1} — ?$
Показать решение и ответ
Скрыть
Решение:Сопротивление проводника рассчитывается по формуле $R = \frac{\rho \cdot l}{S}$.
Сопротивление первого провода: $R_1 = \frac{\rho_1 l_1}{S_1} = \frac{\rho l_1}{S}$.
Сопротивление второго провода: $R_2 = \frac{\rho_2 l_2}{S_2} = \frac{\rho l_2}{S}$.
Теперь сравним их между собой: $\frac{R_2}{R_1} = \frac{\frac{\rho l_2}{S}}{\frac{\rho l_1}{S}} = \frac{l_2}{l_1}$.
Подставим численные значения длины проводов: $\frac{R_2}{R_1} = \frac{1.6 \space м}{0.2 \space м} = 8$.
Получается, что сопротивление второго провода больше сопротивления первого в 8 раз.
Это логично, ведь вы знаете, что чем больше длина проводника, тем больше его сопротивление.
Ответ: сопротивление второго провода больше сопротивления первого в 8 раз.
Упражнение №2
Рассчитайте сопротивления следующих проводников, изготовленных:
- Из алюминиевой проволоки длиной $80 \space см$ и площадью поперечного сечения $0.2 \space мм^2$
- Из никелиновой проволоки длиной $400 \space см$ и площадью поперечного сечения $0.5 \space мм^2$
- Из константановой проволоки длиной $50 \space см$ и площадью поперечного сечения $0.005 \space см^2$
Для решения этой задачи нам понадобятся табличные значения удельного сопротивления для веществ, из которых изготовлены проволоки. Удельное сопротивление алюминия — $0.028 \frac{Ом \cdot мм^2}{м}$, никелина — $0.4 \frac{Ом \cdot мм^2}{м}$, константана — $0.5 \frac{Ом \cdot мм^2}{м}$.
Обратите внимание на единицы измерения удельных сопротивлений, длин и площадей проводников. Для корректных расчетов длину каждой проволоки мы переведем в СИ (в $м^2$). Площади поперечных сечений должны быть выражены в $мм^2$. Для третьего задания переведем $см^2$ в $см^2$.
Дано: $l_1 = 80 \space см$ $l_2 = 400 \space см$ $l_3 = 50 \space см$ $S_1 = 0.2 \space мм^2$ $S_2 = 0.5 \space мм^2$ $S_3 = 0.005 \space см^2 = 0.5 \space мм^2$ $\rho_1 = 0.028 \frac{Ом \cdot мм^2}{м}$ $\rho_2 = 0.4 \frac{Ом \cdot мм^2}{м}$ $\rho_3 = 0.5 \frac{Ом \cdot мм^2}{м}$
СИ: $l_1 = 0.8 \space м$ $l_2 = 4 \space м$ $l_3 = 0.5 \space м$
$R_1 — ?$ $R_2 — ?$ $R_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета сопротивления проводника: $R = \frac{\rho l}{S}$. Рассчитаем по ней сопротивление каждого проводника.
$R_1 = \frac{\rho_1 l_1}{S_1}$, $R_1 = \frac{0.028 \frac{Ом \cdot мм^2}{м} \cdot 0.8 \space м}{0.2 \space мм^2} = \frac{0.0224 \space Ом}{0.2} = 0.112 \space Ом$.
$R_2 = \frac{\rho_2 l_2}{S_2}$, $R_2 = \frac{0.4 \frac{Ом \cdot мм^2}{м} \cdot 4 \space м}{0.5 \space мм^2} = \frac{1.6 \space Ом}{0.5} = 3.2 \space Ом$.
$R_3 = \frac{\rho_3 l_3}{S_3}$, $R_2 = \frac{0.5 \frac{Ом \cdot мм^2}{м} \cdot 0.5 \space м}{0.5 \space мм^2} = \frac{0.25 \space Ом}{0.5} = 0.5 \space Ом$.
Ответ: $R_1 = 0.112 \space Ом$, $R_2 = 3.2 \space Ом$, $R_3 = 0.5 \space Ом$.
Упражнение №3
Спираль электрической плитки изготовлена из нихромовой проволоки длиной $13.75 \space м$ и площадью поперечного сечения $0.1 \space мм^2$. Плитка рассчитана на напряжение $220 \space В$. Определите силу тока в спирали плитки.
Удельное сопротивление нихрома равно $1.1 \frac{Ом \cdot мм^2}{м}$.
Дано: $l = 13.75 \space м$ $S = 0.1 \space мм^2$ $U = 220 \space В$ $\rho = 1.1 \frac{Ом \cdot мм^2}{м}$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Силу тока в спирали плитки мы можем рассчитать, используя формулу закона Ома для участка цепи: $I = \frac{U}{R}$.
Неизвестное сопротивление нихромовой проволоки рассчитаем по формуле $R = \frac{\rho l}{S}$. $R = \frac{1.1 \frac{Ом \cdot мм^2}{м} \cdot 13.75 \space м}{0.1 \space мм^2} = \frac{15.125 \space Ом}{0.1} = 151.25 \space Ом$.
Рассчитаем теперь силу тока: $I = \frac{220 \space В}{151.25 \space Ом} \approx 1.5 \space А$.
Ответ: $I \approx 1.5 \space А$.
Почему у металлов самые низкие удельные сопротивления
Из приведенной таблицы видно, что самыми низкими значениями удельных сопротивлений обладают металлы: серебро, медь, золото, алюминий и др. Такое свойство металлов связано с большой концентрацией свободных электронов, “не привязанных” к конкретному атому, а блуждающих в пространстве кристаллической решетки. Напряжение, приложенное к концам проводника, создает электрическое поле, которое действует на электроны, заставляя их двигаться согласованно, в одном направлении.
Рис. 2. Электрический ток в металлах, свободные электроны.
Самым низким значением ρ обладает серебро — 0,016 Ом*мм2/м. Но для повсеместного, массового, использования в сетях электроснабжения и оборудовании этот металл не используется в виду слишком большой цены. Серебро применяется для создания самых ответственных контактов в специальных электротехнических устройствах. В следующей таблице приведены величины удельных сопротивлений металлов и сплавов, часто используемых металлов в электротехнике:
Таблица
Удельные сопротивления металлов, Ом*мм2/м
(при Т = 200С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Наиболее популярными в электротехнике являются медь и алюминий. Медь и медные сплавы применяются для изготовления кабельной продукции и шунтов — деталей, ограничивающих большие токи через измерительные приборы.
Влияние температуры на удельное сопротивление
В справочниках значения ρ металлов приводятся при комнатной температуре 200С. Но эксперименты показали, что зависимость ρ(Т) имеет линейный характер и описывается формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (3),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α— температурный коэффициент сопротивления, который тоже имеет тоже индивидуален для каждого вещества. Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
- Серебро — 0,0035;
- Медь — 0,004;
- Алюминий — 0,004;
- Железо — 0,0066;
- Платина — 0,0032;
- Вольфрам — 0,0045.
Таким образом, при повышении температуры сопротивление металлов растет. Это объясняется тем, что с ростом температуры увеличивается число дефектов в кристаллической решетке из-за более интенсивных тепловых колебаний ионов, тормозящих электронный ток.
Температурная зависимость удельного сопротивления металлов.
При приближении температуры металла к абсолютному нулю удельное сопротивление резко падает до нуля. Это явление называется сверхпроводимостью, а материалы, обнаруживающие такую способность, называются сверхпроводниками. Этот эффект открыл в 1911 г. голландский физик Камерлинг-Оннес. В его эксперименте удельное сопротивление ртути уменьшилось до нуля при 4,10К.
Проводимость и сопротивление
У.с. показывает способность вещества препятствовать прохождению тока. Но в физике есть и обратная величина — проводимость. Она показывает способность проводить электрический ток. Выглядит она так:
σ=1/ρ, где ρ — это и есть удельное сопротивление вещества.
Если говорить о проводимости, то она определяется характеристиками носителей зарядов в этом веществе. Так, в металлах есть свободные электроны. На внешней оболочке их не больше трех, и атому выгоднее их «отдать», что и происходит при химических реакциях с веществами из правой части таблицы Менделеева. В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В растворах носителями заряда являются ионы.
Если говорить о таких веществах, как кремний, то по своим свойствам он является полупроводником и работает несколько по иному принципу, но об этом позже. А пока разберемся, чем же отличаются такие классы веществ, как:
- Проводники;
- Полупроводники;
- Диэлектрики.
Проводники и диэлектрики
Есть вещества, которые ток почти не проводят. Они называются диэлектриками. Такие вещества способны поляризоваться в электрическом поле, то есть их молекулы могут поворачиваться в этом поле в зависимости от того, как распределены в них электроны. Но поскольку электроны эти не являются свободными, а служат для связи между атомами, ток они не проводят.
Проводимость диэлектриков почти нулевая, хотя идеальных среди них нет (это такая же абстракция, как абсолютно черное тело или идеальный газ).
Условной границей понятия «проводник» является ρ<10^-5 Ом, а нижний порог такового у диэлектрика — 10^8 Ом.
Между этими двумя классами существуют вещества, называемые полупроводниками. Но выделение их в отдельную группу веществ связано не столько с их промежуточным состоянием в линейке «проводимость — сопротивление», сколько с особенностями этой проводимости в различных условиях.
Зависимость от факторов внешней среды
Проводимость — не совсем постоянная величина. Данные в таблицах, откуда берут ρ для расчетов, существуют для нормальных условий среды, то есть для температуры 20 градусов. В реальности для работы цепи сложно подобрать такие идеальные условия; фактически у.с. (а стало быть, и проводимость) зависят от следующих факторов:
- температура;
- давление;
- наличие магнитных полей;
- свет;
- агрегатное состояние.
Разные вещества имеют свой график изменения этого параметра в разных условиях. Так, ферромагнетики (железо и никель) увеличивают его при совпадении направления тока с направлением силовых линий магнитного поля. Что касается температуры, то зависимость здесь почти линейная (существует даже понятие температурного коэффициента сопротивления, и это тоже табличная величина). Но направление этой зависимости различно: у металлов оно повышается с повышением температуры, а у редкоземельных элементов и растворов электролитов увеличивается — и это в пределах одного агрегатного состояния.
У полупроводников зависимость от температуры не линейная, а гиперболическая и обратная: при повышении температуры их проводимость увеличивается. Это качественно отличает проводники от полупроводников. Вот так выглядит зависимость ρ от температуры у проводников:
Здесь представлены удельное сопротивление меди, платины и железа. Немного другой график у некоторых металлов, например, ртути — при понижении температуры до 4 К она теряет его почти полностью (такое явление называется сверхпроводимостью).
А для полупроводников эта зависимость будет примерно такая:
При переходе в жидкое состояние ρ металла увеличивается, а вот дальше все они ведут себя по-разному. Например, у расплавленного висмута оно ниже, чем при комнатной температуре, а у меди — в 10 раз выше нормального. Никель выходит из линейного графика еще при 400 градусах, после чего ρ падает.
Зато у вольфрама температурная зависимость настолько высока, что это становится причиной перегорания ламп накаливания. При включении ток нагревает спираль, и ее сопротивление увеличивается в несколько раз.
Также у. с. сплавов зависит от технологии их производства. Так, если мы имеем дело с простой механической смесью, то сопротивление такого вещества можно посчитать по среднему, а вот оно же у сплава замещения (это когда два и более элемента складываются в одну кристаллическую решетку) будет иным, как правило, куда большим. Например, нихром, из которого делают спирали для электроплиток, имеет такую цифру этого параметра, что этот проводник при включении в цепь греется до красноты (из-за чего, собственно, и используется).
Вот характеристика ρ углеродистых сталей:
Как видно, при приближении к температуре плавления оно стабилизируется.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект. Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10-20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Медь
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м3. Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Будет интересно➡ Сила электрического тока и все о нем
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
Медные провода
При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
Понятие сопротивления
Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Применение медных проводников
Медь является не только хорошим проводником электрического тока, но и очень пластичным материалом. Благодаря этому свойству медная проводка лучше укладывается, она устойчива к изгибам и растяжению.
Медь очень востребована на рынке. Из этого материала производят множество различных изделий:
- Огромное многообразие проводников;
- Автозапчасти (например, радиаторы);
- Часовые механизмы;
- Компьютерные составляющие;
- Детали электрических и электронных приборов.
Удельное электрическое сопротивление меди является одним из лучших среди проводящих ток материалов, поэтому на ее основе создается множество товаров электроиндустрии. К тому же медь легко поддается пайке, поэтому очень распространена в радиолюбительстве.
Высокая теплопроводность меди позволяет использовать ее в охлаждающих и обогревающих устройствах, а пластичность дает возможность создавать мельчайшие детали и тончайшие проводники.
Что влияет на сопротивление медного провода
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.
Зависимость сопротивления
Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.
Таблица удельного сопротивления
Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.
Выводы
Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.
Температурная корреляция
Таблица удельного электрического сопротивления некоторых металлов
| Вид провода | ρ при 20℃, Ом-м |
| Серебряный | 1,59×10⁻⁸ |
| Медный | 1,67×10⁻⁸ |
| Золотой | 2,35×10⁻⁸ |
| Алюминиевый | 2,65×10⁻⁸ |
| Вольфрамовый | 5,65×10⁻⁸ |
| Никелевый | 6,84×10⁻⁸ |
| Железный | 9,7×10⁻⁸ |
| Платиновый | 1,06×10⁻⁷ |
| Стальной | 1,6×10⁻⁷ |
| Свинцовый | 2,06×10⁻⁷ |
| Дюралюминиевый | 4,0×10⁻⁷ |
| Нихромовый | 1,05×10⁻⁶ |
Удельное сопротивление абсолютно независимо от формы и размеров проводника, однако варьируется в широком диапазоне при отклонении температуры от принятого за стандартное значения, равного 20 градусам Цельсия. Практическим электротехническим путем доказано, что увеличение температуры повышает сопротивляемость металлов течению тока, с обратной стороны — вместе со снижением температуры она снижается. Примерно подсчитать, насколько существенным будет изменение, можно с учетом того, что всем металлам присущ почти одинаковый уровень прироста убыли данной величины, в среднем составляющий 0,4% на 1°С.
График сопротивления
Если же данный показатель нужно определить точно, то можно воспользоваться этой формулой:
ρ = ρ0 x (1 + α x (t — t))
, где ρ и ρ0 — соответственно удельные сопротивления при температурах t и t (20°С, табличное значение), α — температурный коэффициент сопротивления.
| Вид провода | α |
| Никелевый | 0,005866 |
| Железный | 0,005671 |
| Молибденовый | 0,004579 |
| Вольфрамовый | 0,004403 |
| Алюминиевый | 0,004308 |
| Медный | 0,004041 |
| Серебряный | 0,003819 |
| Платиновый | 0,003729 |
| Золотой | 0,003715 |
| Цинковый | 0,003847 |
| Стальной | 0,003 |
| Нихромовый | 0,00017 |
Так, к примеру, найдя в таблицах удельное сопротивление меди при 20 градусах Цельсия и ее температурный коэффициент, можно вычислить, что при нагреве до 100℃ ее сопротивление вырастет на 32%. Практически то же самое будет происходить с удельным сопротивлением алюминиевого кабеля с тем же коэффициентом (0,004). А вот удельное сопротивление стали повысится менее значительно — на 24%.
Нагрев
С увеличением температуры проводник насыщается тепловой энергией, передающейся всем атомам вещества. Этим обуславливается повышение интенсивности их теплового движения. Последний фактор и приводит к повышению сопротивляемости движению свободных электронов в определенном направлении, поскольку возрастает вероятность встречи свободных электронов с атомами. Когда температура снижается, меньшее количество атомов может препятствовать направленному движению электронов, следовательно, происходит обратное. В результате колоссального спада температуры возникает интереснейшее явление, называемое «сверхпроводимостью металлов»: сопротивляемость уменьшается до нуля в условиях, близких к абсолютному нулю (-273,15℃). В таких кондициях атомы металла замирают на своих позициях, и электроны движутся без каких-либо препятствий.
Сверхпроводимость
Сравнение проводимости разных видов стали
Характеристики стали зависят от ее состава и температуры:
- Для углеродистых сплавов сопротивление довольно низкое: оно составляет 0,13-0,2 мкОм/м. Чем выше температура, тем больше значение;
- Низколегированные сплавы имеют более высокое сопротивление — 0,2-0,43 мкОм/м;
- Высоколегированные стали отличаются высоким сопротивлением — 0,3-0,86 мкОм/м;
- Благодаря высокому содержанию хрома сопротивление хромистых нержавеющих сплавов равняется 0,5-0,6 мкОм/м;
- Хромоникелевые аустенитные стали являются нержавеющими и благодаря никелю имеют высокую сопротивляемость — 0,7-0,9 мкОм/м.
Медь стоит на втором месте по степени электропроводимости: она отлично пропускает электрический ток и повсеместно используется при изготовлении проводов. Не реже применяют и алюминий: он слабее меди, но дешевле и легче.
Активное сопротивление проводов, кабелей и линий
Из-за того что переменный ток проходит неравномерно, то при одинаковых условиях тока переменного и постоянного R будет отличаться. Как уже было сказано, стальные электропровода имеют лучшее активное R по сравнению с проводниками из цветных металлов, которые имеют одинаковое R при любой силе тока.
Напротив, активное R электрокабелей из стали всегда зависит от электрического тока, поэтому удельную постоянную проводимость в этом случае никогда не используют. Активное R электрокабеля определяют с помощью формулы: R=l/у*s.
Формулы расчёта электрического сопротивления
Рассмотрим формулы для разных видов сопротивлений.
Формула активного сопротивления
Выглядит следующим образом:
\[ Im=Um/R \]
Формула индуктивного сопротивления
Выгляди как:
\[ Xl=2пFL \]
L представляет собой показатель переменного тока.
F представляет собой частоту
Формула ёмкостного сопротивления
Проводник, подключённый непосредственно к электрической цепи, который не имеет сопротивление, но предусматривает наличие ёмкости.
Выглядит формула так:
\[ Xc = 1/ωC \]
- ω показатель циклической частоты.
- C показатель ёмкости.
Определение полного сопротивления
Чтобы получить данное значение, потребуется учесть сопротивление всех участков.
Выглядит так:
\[ R=R1+R2 \]
При этом участков может быть несколько.