- Уравнения и графики
- Обоснование векторной диаграммы
- Действующая величина переменного тока
Синусоидальные э.д.с. и ток:
Получение, передача и использование электрической энергии осуществляются в основном с помощью устройств и сооружений переменного тока. Для этого применяют генераторы, трансформаторы, линии передачи и распределительные сети переменного тока. Наиболее широко применяют приемники электрической энергии, работающие на переменном токе. Переменным электрическим током называется электрический ток, изменяющийся с течением времени (см. рис. 2.1, кривые 2, 3).
Периодический электрический ток, являющийся синусоидальной функцией времени, называется синусоидальным электрическим током.
Такой ток в практике обычно имеют в виду, когда говорят о переменном токе. В некоторых случаях ток изменяется по периодическому несинусоидальному закону.
В линейных электрических цепях переменный синусоидальный ток возникает под действием э. д. с. такой же формы. Поэтому для изучения электрических устройств и цепей переменного тока необходимо прежде рассмотреть способы получения синусоидальной э. д. с. и основные понятия, относящиеся к величинам, которые изменяются по синусоидальному закону.
Получение синусоидальной э.д.с.
Для получения э. д. с. синусоидальной формы генератор переменного тока промышленного типа имеет определенные конструктивные особенности. Однако принципиально синусоидальную зависимость э. д. с. от времени можно получить, вращая с постоянной частотой в равномерном магнитном поле проводник в виде прямоугольной рамки (рис. 12.1).
Рис. 12.1. Прямоугольная рамка в магнитном поле
Вращение витка в равномерном магнитном поле
Согласно формуле (10.5), э. д. с. в рамке, имеющей два активных проводника длиной l,
При равномерном вращении рамки линейная скорость проводника не изменяется: а угол между направлением скорости и направлением магнитного поля изменяется пропорционально времени: Угол β определяет положение вращающейся рамки относительно плоскости, перпендикулярной направлению магнитной индукции. (Положение рамки в момент начала отсчета времени t = 0 характеризуется углом β = 0.) Поэтому э. д. с. в рамке является синусоидальной функцией времени Наибольшей величины э. д. с. достигает при угле В рассмотренном случае синусоидальное изменение э. д. с. достигается за счет непрерывного изменения угла, под которым проводники пересекают линии магнитной индукции. Однако такой способ получения э. д. с. в практике не применяется, так как трудно создать равномерное поле в достаточно большом объеме.
Генератор переменного тока
В электромашинных генераторах переменного тока промышленного типа синусоидальная э. д. с. получается при постоянном угле, но в неравномерном магнитном поле.
Магнитное поле генератора (радиальное) в воздушном зазоре между статором и ротором направлено по радиусам окружности ротора (рис. 12.2, а). Магнитная индукция вдоль воздушного зазора распределена по закону, близкому к синусоидальному. Такое распределение достигается соответствующей формой полюсных наконечников. Синусоидальный закон распределения магнитной индукции вдоль воздушного зазора показан на рис. 12.2, б в развернутом виде.
Рис. 12.2. Схема генератора переменного тока. Распределение магнитной индукции вдоль воздушного зазора
Рис. 12.3. Схема генератора переменного тока с двумя парами полюсов на роторе
Рис. 12.4. Схема генератора с тремя витками (обмотками)
В любой точке воздушного зазора, положение которой определяется углом β, отсчитанным от нейтральной плоскости (нейтрали) против движения часовой стрелки, магнитная индукция выражается уравнением
Нейтральная плоскость перпендикулярна оси полюсов и делит магнитную систему на симметричные части, из которых одна относится к северному полюсу, а другая — к южному.
Наибольшую величину магнитная индукция имеет под серединой полюсов, т. е. при углах и На нейтрали (при β = 0 и β = 180°) магнитная индукция равна нулю (В = 0). На рис. 12.3 показана конструктивная схема генератора переменного тока с двумя парами полюсов, расположенных на роторе, а проводники обмотки, где наводится э. д. с., помещены в пазах сердечника статора.
Отметим еще одну разновидность генераторов переменного тока — генератор с тремя обмотками (трехфазный генератор), которые на схеме рис. 12.4 представлены тремя витками на роторе (у турбогенераторов и гидрогенераторов эти обмотки находятся на статоре). Плоскости витков находятся под углом 120° друг к другу.
Э.Д.С. в обмотке генератора
При равномерном вращении ротора в его обмотке (на рис. 12.2, а — в витке) наводится э. д. с., определяемая формулой (10.4), Подставляя выражение магнитной индукции (12.3), получим
При β = 90°, т. е. в положении проводника под серединой полюса, наводится наибольшая э. д. с. Уравнение э. д. с. можно записать так: Учитывая формулу (12.1), получим такую же зависимость э.д.с. от времени, как при вращении рамки (см. рис. 12.1), считая начальным положение витка (t = 0), когда его плоскость совпадает с нейтралью: Таким образом, и в данном случае э. д. с. является синусоидальной функцией времени (рис. 12.5). Такой же результат получается, если вращать полюса, а проводники оставить неподвижными.
Рис. 12.5. График синусоидальной э. д. с.
В прямоугольной системе координат э. д. с. можно изобразить в функции угла или в функции времени t. Зависимость и можно изобразить одной кривой, но при разных масштабах по оси абсцисс, отличающихся в ω раз. Если обмотку генератора замкнуть через сопротивление, то в образовавшейся цепи возникает синусоидальный ток, повторяющий по форме кривую э. д. с. Полагая сопротивление цепи линейным, равным R, получим для тока такое выражение: где — наибольшая величина тока. Напряжение и ток синусоидальной формы можно получить при помощи генераторов, не имеющих вращающихся частей и магнитных полюсов, например ламповых генераторов.
Задача 12.1.
Э. д. с. электромашинного генератора выражается уравнением . Определить число пар полюсов этого генератора, если известна частота вращения ротора n = 75 об/мин. На какой угол в пространстве поворачивается ротор генератора за 1/4 периода? Решение. Период э. д. с., наводимой в обмотке генератора (см. рис. 12.2), имеющего одну пару полюсов, равен времени полного оборота ротора. Угловую скорость вращения ротора можно определить отношением полного угла, соответствующего одному обороту ротора, к периоду: Однако генератор может иметь не одну, а p пар полюсов (на рис. 12.3 p = 2). Полный цикл изменения э. д. с. в этом случае совершается при движении проводника мимо одной пары полюсов (как за полный оборот ротора в генераторе с p = 1), поэтому при одинаковой частоте вращения ротора период э.д. с. будет в p раз короче, а частота в р раз больше. Уменьшение периода и соответствующее увеличение частоты при данном числе пар полюсов можно получить, увеличивая частоту вращения ротора. Частота синусоидальной э. д.с. при р = 1 равна числу оборотов ротора в секунду, а при р > 1 где n — частота вращения ротора, об/мин. Из уравнения э. д. с. известна угловая частота ω = 314 рад/с; при этом При частоте вращения ротора n = 75 об/мин
При р = 1 за 1/4 периода ротор повернется на 1/4 окружности, т. е. в угловой мере на 90º. При р = 40 угол поворота ротора за 1/4 периода будет в р раз меньше:
Уравнения и графики синусоидальных величин
Анализ электрических цепей переменного тока невозможно проводить без выражения э. д. с. токов, напряжений их уравнениями. Для наглядности применяются графики этих величин в прямоугольной системе координат. Поэтому рассмотрим уравнения и графики синусоидальных величин более подробно.
Уравнения и графики
Уравнение (12.4) записано для случая, когда начало отсчета времени (t = 0) совпадает с моментом прохождения витка через нейтраль (на рис. 12.2, а положение 1, в котором плоскость витка совпадает с нейтралью).
На рис. 12.4 положение витков тоже соответствует началу отсчета времени (t = 0) и определяется для каждого из них углом, отсчитанным от нейтрали до плоскости витка: для первого витка этот угол для второго — и третьего — При вращении ротора э. д. с. будет наводиться во всех витках, но уравнения э.д.с. не будут одинаковыми. Действительно, при = 0 э. д. с. в витках: Эта зависимость э. д. с. от начального положения витка учитывается введением в уравнение начального угла. С учетом начального угла э. д. с. витка С выражается уравнением
э. д. с. витка B
Таким образом, в общем виде, уравнение э. д. с. должно быть записано так:
Из этого уравнения можно определить величину э. д. с. в любой момент при произвольном начальном положении витка. На рис. 12.6 в соответствии с уравнением (12.6) построены графики э.д.с.трех витков, отличающихся в момент начала отсчета времени расположением относительно нейтральной плоскости (eA при eC при eB при ).
Рис. 12.6. Графики э. д. с., сдвинутых по фазе
Характеристики синусоидальных величин
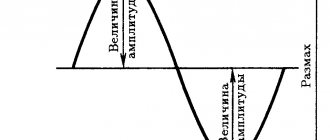
Уравнением и графиком задаются все характеристики синусоидально изменяющейся величины: амплитуда, угловая частота, начальная фаза, период, частота и для любого момента времени мгновенная величина.
Далее приведены определения этих характеристик, и они показаны на рис. 12.7 применительно к синусоидальной э. д. с. Определения распространяются на все величины, изменяющиеся по синусоидальному закону (ток, напряжение и др.).
Рис. 12.7. К вопросу о характеристиках периодической э. д. с.
Мгновенная величина (или мгновенное значение) э. д. с. е — величина э. д. с. в рассматриваемый момент времени. Мгновенная э. д. с. определяется уравнением (12.6) при подстановке в него времени t, прошедшего от начала отсчета до данного момента.
Период Т — наименьший интервал времени, по истечении которого мгновенные величины периодической э. д. с.. повторяются. Если аргумент синусоидальной функции выражается в углах, то период выражается постоянной величиной 2π. Частота f — величина, обратная периоду: т. е. частота равна числу периодов переменной э. д. с. в секунду. Частота выражается в герцах (Гц): 1 Гц = 1/с. Амплитуда Еm — наибольшая величина, которую принимает э. д. с. в течение периода. Амплитуда является одной из мгновенных величин, которая соответствует аргументу равному , где k — любое целое число или нуль. Фаза (фазовый угол ) — аргумент синусоидальной э.д.с., отсчитываемый от ближайшей предшествующей точки перехода э. д. с. через нуль к положительному значению. Фаза в любой момент времени определяет стадию гармонического изменения синусоидальной э. д. с. Начальная фаза ψ — фаза синусоидальной э.д.с. в начальный момент времени. Две синусоидальные величины, имеющие разные начальные фазы, называются сдвинутыми по фазе. Угловая частота ω — скорость изменения фазы. За время одного периода Т фазовый угол равномерно изменяется на 2π, поэтому
Задача 12.4.
Переменный электрический ток задан уравнением
Определить период, частоту этого тока и мгновенные величины его при t = 0; t1 = 0,152 с. Построить график тока. Решение. Уравнение синусоидального тока в общем случае имеет вид Сопоставляя это уравнение с заданным частным уравнением тока, устанавливаем, что амплитуда Im = 100 А, угловая частота ω = 628 рад/с, начальная фаза ψ = —60°. Период Частота
Рис. 12.8. К задаче 12.4
Мгновенные величины тока найдем, подставив в уравнение тока заданные значения времени:
при t = 0 при t1 = 0,152 с Синусоидальная величина через 360° повторяется, поэтому мгновенный ток при угле будет таким же, как и при угле : Для построения графика нужно определить ряд мгновенных токов, соответствующих различным моментам времени (рис. 12.8).
Векторные диаграммы
До сих пор величины, изменяющиеся по синусоидальному закону, задавали уравнениями и изображали графиками в прямоугольной системе координат. При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.
Обоснование векторной диаграммы
Предположим, что ток задан уравнением Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Рис. 12.10. К вопросу о векторной диаграмме
Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени. Например, для t = t1 в общем случае Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж: в начальном положении.
Построение векторной диаграммы
Вращая вектор Im’ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой. Например, напряжение и ток в электрической цепи выражаются уравнениями
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока то
Рис. 12.11. Векторная диаграмма тока и напряжения
Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Сложение и вычитание векторов
Простота и наглядность векторных диаграмм — не единственное и не главное достоинство способа изображения синусоидальных величин. Требуется сложить, например, два тока, заданных уравнениями Выражение суммы оказывается громоздким, из него не видны амплитуда и начальная фаза результирующего тока.
Можно графически сложить два заданных тока, построив их в одной системе координат и для ряда аргументов, найдя сумму двух ординат. Через полученные точки проведем кривую суммы, увидим, что эта кривая тоже синусоида с таким же периодом, как и слагаемые. По кривой общего тока можно найти амплитуду и начальную фазу. Громоздкость и неудобство такого сложения очевидны.
Очень просто сложение и вычитание синусоидальных величин осуществляется по правилам сложения и вычитания векторов.
Рис. 12.12. Сложение векторов
Сложим два заданных тока i1 и i1 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллельно самим себе так, чтобы начало последующего вектора совпало с концом предыдущего. Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора — уменьшаемого и обратного — вычитаемого (рис. 12.13):
Рис. 12.13. Вычитание векторов
Рис. 12.14. Частные случаи сложения векторов
При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Задача 12.7. Два тока заданы уравнениями
Найти уравнения токов: Решение. Решение задачи проще всего выполнять графически в векторной форме. Для этого изобразим векторы заданных токов. Масштаб тока выбираем так, чтобы наибольший вектор поместился на имеющемся листе бумаги, одновременно учитывая возможность отчетливого изображения наименьшего вектора. При разборе решения рекомендуется провести построения по рис. 12.15 на листе миллиметровой бумаги в масштабе В этом масштабе длина векторов
Длину вектора суммы определяют графически (рис. 12.15, а):
Рис. 12.15. К задаче 12.7
Начальная фаза этого вектора по чертежу Уравнение суммы токов В таком же порядке найдены векторы разностей токов (рис. 12.15, б, в). Вычитаемые векторы взяты в противофазе с заданными. После измерения длин векторов и начальных фаз напишем уравнения разностей токов:
Переменный ток. Изображение синусоидальных переменных.
Представление синусоидальных величин с помощью векторов и комплексных чисел
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,
а наименьший промежуток времени, через который эти повторения наблюдаются, —
периодом Т.
Для периодического тока имеем
| , | (1) |
Величина, обратная периоду, есть частота,
измеряемая в герцах (Гц):
| , | (2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01?10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ? 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f
= 50Гц
.
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i
— мгновенное значение тока ;
u —
мгновенное значение напряжения ;
e
— мгновенное значение ЭДС ;
p — мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
— амплитуда тока;
— амплитуда напряжения;
— амплитуда ЭДС.
Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением
периодического тока:
| , | (3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1
и
е2
соответствуют уравнения:
.
Значения аргументов синусоидальных функций и называются фазами
синусоид, а значение фазы в начальный момент времени
(t=0):
и —
начальной фазой
( ).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой.
Так как фазовый угол синусоиды за время одного периода
Т
изменяется на рад., то угловая частота есть , где
f–
частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз
.
Для синусоидальных ЭДС е1
и
е2
угол сдвига фаз:
.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное
) с угловой частотой, равной
w
. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС
е1
и
е2
(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют
векторными диаграммами.
При построении векторных диаграмм векторы удобно располагать для начального момента времени
(t=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью
w
. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
и .
Результирующий ток также будет синусоидален:
.
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0.
При вращении этих векторов с одинаковой угловой скоростью
w
их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Представление синусоидальных ЭДС, напряжений и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической
или
алгебраической
—
формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
.
Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
| , | (4) |
Комплексное число удобно представить в виде произведения двух комплексных чисел:
| , | (5) |
Параметр , соответствующий положению вектора для t=0
(или на вращающейся со скоростью
w
комплексной плоскости), называют
комплексной амплитудой:
, а параметр —
комплексом мгновенного значения.
Параметр является оператором поворота
вектора на угол
wt
относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a
.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j”
произведения комплекса амплитуды и оператора поворота :
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
| , | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
,
— то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:
.
Тогда мгновенное значение напряжения:
,
где .
При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)
| , | (7) |
а при (третий квадрант)
| (8) |
или
| (9) |
Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:
где ;
.
Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
.
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:
| . | (10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
.
Литература
1. Основы
теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А.
Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
5. На рис. 5 , а . Определить .
Ответ: .
Действующая и средняя величины переменного тока
О переменном токе все известно, если задано его уравнение или график. Однако в практике пользоваться уравнениями или графиками токов затруднительно. Переменный ток обычно характеризуется его действующей величиной I. При изучении выпрямительных устройств и электрических машин пользуются средними величинами э. д. с., тока, напряжения.
Действующая величина переменного тока
При определении действующей величины переменного тока можно исходить из какого-либо его действия в электрической цепи (теплового, механического взаимодействия проводов с токами).
На рис. 12.18 изображены графики двух токов: постоянного 1 и переменного 2, причем величина постоянного тока равна амплитуде переменного. Постоянный ток, равный амплитуде переменного, выделит больше тепла в одном и том же элементе цепи за однj и то же время, так как переменный ток в течение полупериода меньше постоянного, и лишь одно мгновение эти токи равны.
Действующая величина переменного тока I численно равна величине постоянного тока, который в одном и том же элементе цепи за время периода Т выделяет столько же тепла, сколько при тех же условиях выделяет переменный ток.
Действующая величина переменного тока I меньше амплитуды (прямая 3 на рис. 12.18).
Рис. 12.18. К определению действующей величины переменного тока
Определим количество тепла, выделяемого за период Т постоянным током, равным I, и переменным током (см. рис. 12.18) в элементе цепи с сопротивлением R: Приравнивая найдем
Действующая величина периодического тока является его средней квадратичной за период.
Ее можно найти из уравнения (12.9), но для наглядности воспользуемся графическим решением поставленной задачи.
Среднеквадратичную величину переменного тока за период можно представить в виде квадратного корня из суммы очень большого числа ординат кривой i2(t), разделенной на число ординат n: где в числителе подкоренного выражения представлена сумма квадратов ряда мгновенных токов в течение периода, n — число этих значений, стремящееся к ∞. На рис. 12.19 показаны ряд положений вращающегося с угловой скоростью ω вектора тока Im и соответствующие им мгновенные токи i. Эти положения отмечены точками 0, 1, 2 и т. д. на окружности, которую описывает конец вектора Im.
Рассмотрим два положения вектора Im (отмечены точками 2 и 8), отстоящие по окружности на 90°, т. е. находящиеся соответственно в первой и второй четвертях окружности. Прямоугольные треугольники 6′-2-2′ и 6′-8-8′ равны, так как равны их стороны: 2-2′ = 6′-8′ и 2′-6′ = 8-8′. Из этих треугольников следует:
Рис. 12.19. К определению действующей и средней величины синусоидального тока
Каждому положению вектора Im в первой четверти соответствует другое его положение во второй, для которых можно написать аналогичное выражение. Такие рассуждения можно провести для другой полуокружности, т. е. распространить их на второй полупериод тока, причем квадраты отрицательных мгновенных токов будут положительны, поэтому Подставляя это выражение в (12.10), получим Таким образом, действующая величина синусоидального тока меньше его амплитуды в раза.
Понятие о действующей величине можно распространить на все синусоидальные функции и, следовательно, говорить о действующей величине напряжения, э. д. с.
Действующие величины тока, напряжения измеряются электроизмерительными приборами. Номинальные токи и напряжения электротехнических устройств выражаются действующими величинами. Введя понятие о действующей величине, в дальнейшем векторные диаграммы будем строить для действующих величин напряжений и токов.
Отношение амплитуды к действующей величине называется коэффициентом амплитуды Ка. Для синусоидальной функции этот коэффициент равен ; если кривая тока или напряжения имеет более острую форму, чем синусоида, то Ка > , в противном случае Ка (при прямоугольной форме Ка = 1).
Частные случаи значений амплитуды силы тока
В том случае, если цепь состоит только из активного сопротивления $(R)$, тогда:
ток совпадает с напряжением по фазе, амплитуда силы тока в этом случае равна:
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Если сравнивать уравнение (6) с выражением (3), то можно сделать вывод о том, что если вместо конденсатора участок цепи просто закоротить, то это будет означать переход к емкости равной бесконечности.
Пусть в контуре можно сопротивлением пренебречь $(R=0)$, а емкость считать равной бесконечности, тогда:
Величину $X_L$ называют реактивным индуктивным сопротивлением (индуктивным сопротивлением), если она равна:
Из формулы следует, что индуктивность постоянному току не сопротивляется (при $\omega$=0, $X_L$=0).
Допустим, что $R=0,\ L=0.$ Тогда согласно формуле (3), получим:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор.
В том случае, если R=0, амплитуда силы тока равна:
Реактивным сопротивлением (реактансом) $(X)$ называют величину равную: