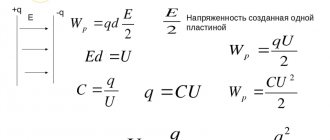Как разрядить конденсатор: самые действенные способы

Разряжаем отверткой

Для начала нам нужна подходящая отвертка с изолирующей рукояткой. Как правило, рукоятки выполнены из резины или пластика. Оба материала способны создать безопасный барьер между рукой металлической частью отвертки.
Если нет уверенности в том, что у вас именно изолирующая отвертка, рекомендуется купить новую, на которой есть логотип с предельно допустимым напряжением.

Такие инструменты продаются в отделах электротоваров в любом хозяйственном отделе. Подойдёт как плоская, так и крестовая отвертка.

Теперь сам процесс разряда.

Возьмите элемент одной рукой у основания, не сильно сжимая;
На оба вывода положить отвертку;
Будет слышен звук разряда и небольшое искрение.

Держите отвертку так, чтобы она касалась обеих ножек одновременно, только тогда процесс разряда произойдёт нормально.

Для контроля можно замкнуть выводы отверткой еще раз.

Проверить степень разрядки можно все тем же мультиметром.

Сначала лучше проверить

Для начала этот элемент нужно обесточить. Понятно, что не надо именного его лишать источника питания. Достаточно отключить электроприбор и отсоединить вилку от розетки. Если подойти к этому вопросу кардинально, то для безопасности можно на распредщитке отключить все автоматические выключатели, отвечающие за подачу электричества в помещение.

Теперь нам нужен специальный прибор — мультиметр, чтобы узнать заряжен ли конденсатор.

Выбираем режим для измерения напряжения DC (постоянного тока).
Ручку прибора выставляем на максимальный уровень замера напряжения.
Щупы мультиметра подсоединяем к контактам электронного компонента. Из него, как правило, выступают два стержня. Вот именно к ним и нужно присоединить оба щупа детектора. Прижимать нужно достаточно плотно, чтобы на дисплее прибора появились цифровые показания. Нет никакой разницы, какой щуп подводить к какому контакту. Полученное значение получится одинаковым в обоих случаях.

Нам нужно понять какое напряжение на выводах элемента. В зависимости от показаний выбирается и способ разрядки:

Если показания меньше 10 вольт необходимости в разрядке нет.
Если на дисплее замеры в пределах 10–99 вольт, разрядить можно отверткой.
Если значения от 100 вольт и выше рекомендуется применить разрядное устройство.

Разряжаем отверткой

Если нет уверенности в том, что у вас именно изолирующая отвертка, рекомендуется купить новую, на которой есть логотип с предельно допустимым напряжением.

Теперь сам процесс разряда.

Возьмите элемент одной рукой у основания, не сильно сжимая;
На оба вывода положить отвертку;
Будет слышен звук разряда и небольшое искрение.

Для контроля можно замкнуть выводы отверткой еще раз.

Проверить степень разрядки можно все тем же мультиметром.

Параметры и принцип работы

Величина электричества, накапливаемого изделием, а также периоды циклов разрядки и зарядки конденсатора определяются характеристиками, зависящими от типа конкретной модели. Благодаря широким пределам параметров и характеристик данные радиодетали могут успешно применяться для различных целей.

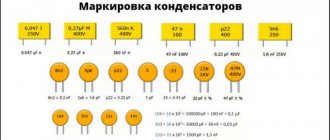
Эти параметры без затруднений определяются по маркировке на корпусе элемента. Конденсаторы, произведенные в России и постсоветском пространстве, в обязательном порядке имеют буквенно-цифровую маркировку, обозначающую технологию и тип, ТКЕ, номинальное напряжение, значение емкости и погрешность производства, а также дату изготовления. Для импортных аналогов характерно только обозначение емкости. На схемах конденсатор изображается двумя параллельными черточками.

Основные и дополнительные параметры:

Емкость (С) – способность радиодетали накапливать электричество (измеряется в фарадах). Емкость самых мощных конденсаторов достигает нескольких десятков фарад.
Удельная емкость – помогает определить отношение емкости к массе или объему изделия (очень важный для микроэлектроники параметр).
Номинальное напряжение (Uн) – позволяет определить предельную величину, при которой конденсатор может эксплуатироваться.
Полярность – важный параметр, несоблюдение которого может привести к выходу радиоэлемента из строя и даже взрыву.
Опасность разрушения – для предотвращения взрыва и замыкания устройство может быть оснащено предохранительным клапаном или специальными насечками на крышке.

Существуют также и паразитные параметры, которые производители стараются снизить при изготовлении продукции. Выбирая радиодетали, следует учитывать стабильность, емкость, ток утечки, рабочее напряжение, точность и температурный коэффициент емкости.

Принцип работы заключается в накоплении электрических зарядов благодаря присутствию диэлектрического материала между металлическими пластинками, на которых собираются электроны и ионы. Проходя через данное устройство, сила тока имеет наибольшее значение и минимальное напряжение, но по мере накопления электроэнергии напряжение возрастает, а сила тока наоборот падает до тех пор, пока не исчезнет совсем. При идеальных условиях время зарядки конденсатора равно нулю.

1.6. Электроемкость. Конденсаторы

Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф):

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля (см. § 1.4).

Рисунок 1.6.1.
Поле плоского конденсатора

Рисунок 1.6.2.
Идеализированное представление поля плоского конденсатора. Такое поле не обладает свойством потенциальности

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением (см. § 1.3)

Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:

Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен

Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы. Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R1 и R2. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:

Таким образом, при параллельном соединении электроемкости складываются.

Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует

Рисунок 1.6.3.
Параллельное соединение конденсаторов. C = C1 + C2

Рисунок 1.6.4.
Последовательное соединение конденсаторов.

При последовательном соединении (рис. 1.6.4) одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них равны и Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2. Следовательно,

При последовательном соединении конденсаторов складываются обратные величины емкостей.

Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.

Модель. Поле плоского конденсатора

Виды и области применения

Существует много способов классификации современных конденсаторов, которые позволяют группировать их в зависимости от типа конструкции, рабочего напряжения, видов поляризации и назначения, изменению емкости, а также разновидности диэлектрика.

Виды поляризации:

ионная и ионно-релаксационная;
объемная;
дипольно-релаксационная;
электронная и электронно-релаксационная;
спонтанная.

Исходя из конструктивных особенностей, различают трубчатые и цилиндрические, монолитные, пластинчатые и секционные, дисковые, горшкообразные и литые, бочоночные, а также секционные разновидности.

Область применения конденсаторов:

Электроника – радиотехническое и телевизионное оборудование, запоминающие устройства, автоматика и разнообразная телемеханика, телеграфия и телефония.
Электроэнергетика – сварка разрядом, запуск электродвигателей, подавление радиопомех, регулирование напряжения, электроосвещение, отбор энергии, использование в сложных схемах и генераторах, а также защита от напряжения.
Промышленность – добывающая, металлургическая и металлообрабатывающая.
Техника – медицинская, лазерная, электроизмерительная, радиолокационная, фотографическая, автотракторная.

В зависимости от изменения емкости различают постоянные, переменные (изменение осуществляется механически или электрически) и подстроечные конденсаторы (изменение осуществляется разово или периодически).

Что такое конденсатор?

Прибор, который накапливает электроэнергию в виде электрических зарядов, называется конденсатором.

Количество электричества или электрический заряд в физике измеряют в кулонах (Кл). Электрическую ёмкость считают в фарадах (Ф).

Уединенный проводник электроёмкостью в 1 фараду — металлический шар с радиусом, равным 13 радиусам Солнца. Поэтому конденсатор включает в себя минимум 2 проводника, которые разделяет диэлектрик. В простых конструкциях прибора — бумага.

Работа конденсатора в цепи постоянного тока осуществляется при включении и выключении питания.Только в переходные моменты меняется потенциал на обкладках.

Конденсатор в цепи переменного тока перезаряжается с частотой, равной частоте напряжения источника питания. В результате непрерывных зарядов и разрядов ток проходит через элемент. Выше частота — быстрее перезаряжается прибор.

Сопротивление цепи с конденсатором зависит от частоты тока. При нулевой частоте постоянного тока величина сопротивления стремится к бесконечности. С увеличением частоты переменного тока сопротивление уменьшается.

Переменный ток

Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока

. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.

Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.

Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.

Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.

Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение

Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.

Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением

Давайте-ка выразим из этой формулы заряд конденсатора:

А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:

Емкость конденсатора у нас является величиной постоянной

. Она определяется
исключительно самим конденсатором
, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость
С
конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением
U
нельзя так поступить!
Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.

А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:

По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.

Рисунок 1 – Поясняющая картинка

На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.

Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения.

Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения
U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.

Пусть напряжение на конденсаторе емкостью C

изменяется по закону синуса вот таким вот образом

Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную

Или можно записать вот так

Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения

. Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с
тригонометрическим кругом
, на нем все это видно очень наглядно.

Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов.

Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости
C
конденсатора, амплитуды приложенного к нему напряжения
U
m и частоты
ω
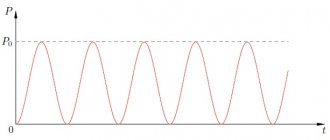
. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).

Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе

На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).

Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t)

через конденсатор емкостью
C
. И закон этот пусть тоже будет синусоидальным

Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:

По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом

Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения

придут вам на помощь, если не понятно, почему получилось именно так.

Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает

напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.

Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.

Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.

Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.

Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.

Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.

Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )

Рисунок 3 – Ищем ток через этот конденсатор

Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.

Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное

значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону

Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так

Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока

Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.

Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.

Рисунок 4 – График напряжения в розетке

Рисунок 5 – График тока через конденсатор

Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Сначала лучше проверить

Теперь нам нужен специальный прибор — мультиметр, чтобы узнать заряжен ли конденсатор.

Выбираем режим для измерения напряжения DC (постоянного тока).
Ручку прибора выставляем на максимальный уровень замера напряжения.
Щупы мультиметра подсоединяем к контактам электронного компонента. Из него, как правило, выступают два стержня. Вот именно к ним и нужно присоединить оба щупа детектора. Прижимать нужно достаточно плотно, чтобы на дисплее прибора появились цифровые показания. Нет никакой разницы, какой щуп подводить к какому контакту. Полученное значение получится одинаковым в обоих случаях.

Если показания меньше 10 вольт необходимости в разрядке нет.
Если на дисплее замеры в пределах 10–99 вольт, разрядить можно отверткой.
Если значения от 100 вольт и выше рекомендуется применить разрядное устройство.

Разрядное устройство своими руками

Перед тем как измерить емкость, проверить кондёры на пробой или утечку, или если нужна замена несправного элемента необходимо его разрядить. Особенно актуально сделать правильный разряд у высоковольтных радиодеталей большой емкости. Накопленная энергия может сохраняться длительное время и неправильный демонтаж или хранение может нести угрозу для жизни.

Для безопасной разрядки высоковольтных конденсаторов можно собрать недорогое, простое в реализации электронное устройство. Оно разряжает вполне эффективно и безопасно.

Посмотрим на его принципиальную схему:

Напряжение с высоковольтного конденсатора поступает на гасящий резистор R1 и далее уходит на диодный ограничитель напряжения двустороннего типа.

Сам диодный ограничитель из двух параллельных цепочек диодов D1-D3 и D4-D6. Это сделано для того чтобы от любого диода в цепи снять напряжение порядка 2 вольт для работы светодиодных индикаторов D7, D8. Поступающий ток на светодиоды ограничивается резистором R2.

Светодиод запускает процесс разряда высоковольтного конденсатора до безопасного напряжения порядка двух вольт.

На процесс разряда может потребоваться некоторое время от 10 сек. и больше. Время разряда зависит от емкости подключенного кондёра и, какое остаточное напряжение в нем оставалось.

Как только светодиод потухнет можно провести окончательный разряд, с помощью отвертки закоротив выводы радиодетали.

Схема вполне работоспособна.

Всю плату можно собрать самостоятельно и поместить в пластиковый корпус.

Способы зарядки и разрядки конденсатора

При зарядке конденсатора энергия источника питания переходит в энергию электрического поля, возникающего между металлическими пластинками радиоэлектронного устройства. Важно учитывать, что на каждом участке цепи существует явное (резистор) или неявное сопротивление (провода, внутреннее сопротивление). В этом случае скорость зарядки конденсатора будет зависеть от его емкости и сопротивления во всей цепи. Процесс считается завершенным, когда подаваемое напряжение по своей величине становится равным напряжению на металлических пластинках.

Процесс зарядки и разрядки конденсатора лучше всего определяется мультиметром или при помощи специального измерительного прибора – индикаторной отвертки.

Можно зарядить конденсатор через лампочку. Для этого потребуется подключить «плюс» к аккумулятору через автомобильную лампочку, а «минус» подключить к массе (кузов автомобиля). Лампочка вспыхнет и погаснет. Таким же образом можно зарядить конденсатор для сабвуфера, если он не имеет системы контроля зарядного тока. Данная схема зарядки конденсатора эффективна, проста и безопасна.

Разрядка может понадобиться при ремонте бытовых приборов и электронных устройств. Это можно сделать при помощи отвертки с изолированной рукояткой, поочередно замыкая контакты, одновременно с этим касаясь массы стержнем отвертки. Если конденсатор извлечен из платы, необходимо, не касаясь руками контактов, приложить стержень отвертки к обеим клеммам изделия (должна появиться искра). Также можно собрать разрядное устройство, припаяв к резистору (на несколько кОм) два провода с зажимами, после чего подсоединить их к клеммам конденсатора. Важно проверять напряжение, чтобы убедиться в разреженности прибора.

Назначение и функции конденсаторов

Конденсатор играет огромную роль как в аналоговой, так и цифровой технике. Они бывают электролитическими и керамическими, и отличаются своими свойствами, но не общей концепцией. Примеры использования:

Фильтрует высокочастотные помехи;
Уменьшает и сглаживает пульсации;
Разделяет сигнал на постоянные и переменные составляющие;
Накапливает энергию;
Может использоваться как источник опорного напряжения;
Создает резонанс с катушкой индуктивности для усиления сигнала.

Примеры использования

В усилителях обычно используются для защиты сабвуферов, фильтрации питания, термостабилизации и разделение постоянной составляющей от переменной. А электролитические в автономных схемах с микроконтроллерами могут долго обеспечивать питание за счет большой емкости.

В данной схеме транзистор VT1 постоянно открыт, чтобы усиливать звук без искажений. Но если вход замнется или на него поступи постоянный ток, то транзистор откроется, перейдет в насыщение и перегреется. Чтобы этого не допустить, нужен конденсатор. С1 позволяет отделить постоянную оставляющую от переменной. Переменный сигнал легко проходит на базу транзистора, а постоянный сигнал не проходит.

С2 совместно с резистором R3 выполняет функцию термостабилизации. Когда усилитель работает, транзистор нагревается. Это может внести искажения в сигнал. Поэтому, резистор R3 помогает удержать рабочую точку при нагреве. Но когда транзистор холодный и стабилизации не требуется резистор может уменьшить мощность усилителя. Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.

Чтобы схема качественно работала, обязательно хорошее питание. Когда схема в пиковые значения потребляет больше тока, то это всегда сильная нагрузка на источник питания. С3 фильтрует помехи по питанию и помогает снизить нагрузку. Чем больше емкость — тем лучше звук, но до определенных значений, все зависит от схемы.

А в блоках питания используется тот же принцип, как и в предыдущей схеме по питанию, но здесь емкость нужна гораздо больше. На этой схеме емкость элеткролита может быть как 1000 мкФ, так и 10 000 мкФ.

Еще на диодный мост можно параллельно включить керамические конденсаторы, которые будут шунтировать схему от высокочастотных наводок и шума сети 220 В.

Фазовые искажения

Конденсатор может искажать переменный сигнал по фазе. Это происходит из-за неверного расчета емкости, общего сопротивления и взаимодействия с другими радиодеталями. Не стоит забывать и о том, что любая радиодеталь имеет как реактивное, так и активное сопротивление.

Источник

Ликбез КО. Лекция №2 Конденсатор.

Конденсатор (ёмкость) Конденсатор (ёмкость)

–элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается –
С
. Напряжение и ток на его контактах связано зависимостью: Величина ёмкости измеряется в фарадах (Ф).
1 фарада
– это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон. 1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6. Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке. Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома. Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.

Дифференцирующая цепочка

применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке. Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход. Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве
фильтра высоких частот (ФВЧ)
. Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют
реактивным сопротивлением конденсатора
, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается
Xc
или
Zc
и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением: Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами,
чем выше частота, тем меньше реактивное сопротивление конденсатора
.

Теперь представьте, что дифференцирующая цепь, это – делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке. То, что изображено, называется амплитудно-частотной характеристикой

, или сокращённо —
АЧХ
. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению
f2
.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр

высокой частоты на конденсаторе и резисторе. Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим –
интегрирующую цепочку
. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если
дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ)
. И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению
f1
. Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.
Параллельное соединение конденсаторов
Общая ёмкость конденсаторов при параллельном соединении равна их сумме.
Последовательное соединение конденсаторов
Величина, обратно пропорциональная общей ёмкости конденсаторов при последовательном соединении равна сумме величин, обратно пропорциональных их ёмкости. Для двух последовательно соединенных конденсаторов их общая ёмкость равна:

Советы и предупреждения

После того как процесс разряда завершен можно обернуть его выводы фольгой, чтобы эта радиодеталь оставалась разряженной. Все конденсаторы со временем могут разрядиться сами через несколько дней, при условии, что они не подключены к внешним источникам питания. Но всегда лучше считать, что они находятся в заряженном состоянии и контрольная разрядка будет совсем не лишней. Необходимо постоянно помнить, что крупные радиодетали, коммутирующие электроэнергию, очень опасны

Для работы с такими радиодеталями требуются профессиональные навыки. При работе с электрическими устройствами всегда необходимо соблюдать меры предосторожности.

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора

. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Разряжаем отверткой

Теперь сам процесс разряда.

Возьмите элемент одной рукой у основания, не сильно сжимая;
На оба вывода положить отвертку;
Будет слышен звук разряда и небольшое искрение.

Для контроля можно замкнуть выводы отверткой еще раз.

Проверить степень разрядки можно все тем же мультиметром.

Характеристики и свойства

К параметрам конденсатора, которые используют для создания и ремонта электронных устройств, относят:

Ёмкость — С. Определяет количество заряда, которое удерживает прибор. На корпусе указывается значение номинальной ёмкости. Для создания требуемых значений элементы включают в цепь параллельно или последовательно. Эксплуатационные величины не совпадают с расчетными.
Резонансная частота — fр. Если частота тока больше резонансной, то проявляются индуктивные свойства элемента. Это затрудняет работу. Чтобы обеспечить расчетную мощность в цепи, конденсатор разумно использовать на частотах меньше резонансных значений.
Номинальное напряжение — Uн. Для предупреждения пробоя элемента рабочее напряжение устанавливают меньше номинального. Параметр указывается на корпусе конденсатора.
Полярность. При неверном подключении произойдет пробой и выход из строя.
Электрическое сопротивление изоляции — Rd. Определяет ток утечки прибора. В устройствах детали располагаются близко друг к другу. При высоком токе утечки возможны паразитные связи в цепях. Это приводит к неисправностям. Ток утечки ухудшает емкостные свойства элемента.
Температурный коэффициент — TKE. Значение определяет, как ёмкость прибора меняется при колебаниях температуры среды. Параметр используют, когда разрабатывают устройства для эксплуатации в тяжелых климатических условиях.
Паразитный пьезоэффект. Некоторые типы конденсаторов при деформации создают шумы в устройствах.

Как он работает

Если разобрать конденсатор, то его устройство довольно простое. Это два электрода разделенные диэлектрическим материалом:

воздухом,
керамическим материалом,
импрегнированной бумагой.

В качестве электродов выступают обкладки конденсатора. Именно в них происходит процесс накопления электрической энергии с того момента как на обкладки подается напряжение. Если напряжение не подается, то под действием электростатического притягивания, накопленная энергия сохраняется на обкладках конденсатора.

Кондёры постоянного типа разделяют на:

Плёночные. Состоят из трехслойной пленки по схеме электрод-диэлектрик-электрод. Плёнка сворачивается и ее помещают в корпус. Имеют широкое применение в электрических схемах приборов бытового назначения.
Керамические. Состоят из керамических пластинок с металлическими электродами. Чтобы их разрядить, лучше применять нагрузку с большим сопротивлением.

За единицу емкости этого элемента принято считать фарад. То есть если у кондёра емкость в 1 фараду, то он способен сгенерировать 1 вольт.

В электронике и электротехнике используются элементы, емкость которых может измеряться:

пикофарадами,
нанофарадами,
микрофарадами,
миллифарадами.

Та емкость, которая указана на корпусе элемента это номинал, который практически получить невозможно. Поэтому на конденсаторе указан процентный допуск его емкости. Это надо понимать как процентное отклонение реального значения от номинального.

Характеристики конденсаторов

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Емкость

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

Вам это будет интересно Определение полярности

Как разрядить высоковольтные неполярные конденсаторы без ущерба самим конденсаторам?

Имеется порядка 450VAC 700мкФ (параллельно соединённые) неважно где и как, главное имеем заряженные конденсаторы и их нужно разрядить. Вариант с замкнутыми выводами сразу мимо – это рано или поздно убьёт конденсаторы, а заряжаться и разряжаться будет часто

Разряд должен происходить за 1-3 минуты максимум

Zero # 2022.09.30 07:01 0

Ответы пользователя:счет 0 : 0 ничего не влепят

Ну дык используй шунт на несколько килоом или около, в чём проблема?

Oxotnick # 2022.09.30 20:45 0

Ответы пользователя:Запросто….

Резистор 100 кОм 2Вт параллельно кондерам

Oлeнькa # 2022.10.01 11:40 0

Ответы пользователя:Балотелли по любому)

а через резистор не пробовали? Время разряда на 95 % (те до 5% остаточного заряда) t = 3 RC

Kradun # 2022.10.01 18:44 0

Ответы пользователя:Двухколесное ****

Это отнюдь не высоковольтные конденсаторы…

DolmakimiOglan # 2022.10.02 01:06 0

Ответы пользователя:Загорится.

Во время работы в сети 220 В, как пускового конденсатора в двигателе, через него пойдет ток не менее 50 А. Емкостное сопротивление конденсатора 700 мкФ будет около 4-5 Ом. Поэтому, игра не стОит свеч. Можно разряжать через резистор Ом на 30,желательно Ватт на 10. В лампе-вспышке используется конденсатор 800 мкФ, 450 В и разряжается он почти коротким замыканием и ничего! Учитывая огромную площадь пластин конденсатора, опасность есть только для подводящих к ним проводников. Да, и то, она, скорее всего, преувеличена.

Elvis # 2022.10.02 06:54 0

Ответы пользователя:Зачем обращать внимание на бывшего шахматиста, у которого поехала крыша?

ну)))) есле надо скажите- аб не отв- прям))))) – прилюдно воот!!!! vivalostioz # 2022.10.02 23:26 0

Ответы пользователя:Бесплатное образование и медицина…практически нет, редкий продукт в редких салатах в редкие праздничные столы)…Яндекс в помощь!

Через резистор 5-10 кОм

BOKSYOR # 2022.10.03 01:05 0

Ответы пользователя:Леди Гага

700мкф/450в???? Две последовательно соединенные лампы ватт на60-100 и вся проблема… или резистор 500ом 10 ватт даже простой проволочный! Искр не увидешь даже зато безболезненно для кандеров и самого резистора… он даже не нагреется.. сам так делал когда ночью паял накопитель а все спали…. кстати: нихера кандеру не будет и от кз !!!Если неполярный! Проверено годами )))

Убeй_Meня_Heжнo # 2022.10.03 05:19 0

Ответы пользователя:Просто воспользовалась случаем для коррекции фигуры – и нашим, и вашим.

Это большая емкость, коротить нельзя, резистор около 10 – 50 ком можно снабдить тиристором, нажал кнопку, и проблемы нет….

Zoot # 2022.10.03 05:51 0

Вопросы пользователя:Почему перед операцией обязательно раздеваться до гола перед студентами, я может не хочу чтобы на меня пялились?Я постоянно нервничаю из-за работы, не сплю толком, худею. Работаю учителем в школе и работа очень стрессоваяЧто лучше i5 8400 или Ryzen 5 2600?

собственно штангой с резистором и разряжают..

ПEPBИ3ЦИK # 2022.10.03 09:33 0

Ответы пользователя:У вас горит крыша – звоните 01! Вам нужна крыша – звоните 02! У вас поехала крыша – звоните 03! Вам нужна……нет.. они сами исчезают куда-то)

Сопротивлением перемкни.

BRIQADIR # 2022.10.04 13:55 0

Ответы пользователя:ненавистью…Найти песню по вашей информации трудно. Попробуйте программы для распознавания музыки онлайн: Tunatic,…Топором по башке

Посовeтую вам почитать вот это

WARLOCK # 2022.10.05 12:17 0

Ответы пользователя:”…люди перестали… ” Люди, представь себе, и не начинали.

2 лампы накаливания 220в 100Вт последовательно. тумблер включил – пошла разрядка, заодно и индикация. Потухли полностью – значит разрядились

KRUTOY # 2022.10.06 00:29 0

Ответы пользователя:Хочет побыстрее, что бы бухнуть в дороге…Смотришь в прицел …целишься …стреляешь .. БИНГОО …а нет промазал ( вот так работает прицел :D…Ооо, его взгляд влюблённых глаз, может испепелить…

Пусковой 700мкф… Это двигатель 7,5 квт. Как у тебя сеть то выдержит. Там пусковым током всю линию просадит, что соседи по всей улице возмутятся….

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля

Wp = qEd

Wp — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

E — напряженность электрического поля [В/м]

d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

Wp = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

Wp = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора

Wp = qU/2

Wp — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

U — напряжение на конденсаторе [В]

Энергия конденсатора

Wp = q2/2C

Wp — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

C — электроемкость конденсатора [Ф]

Энергия конденсатора

Wp = CU2/2

Wp — энергия электростатического поля [Дж]

C — электроемкость конденсатора [Ф]

U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Как рассчитать импеданс в цепи

Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.

Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.

К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.

Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.

Практические расчеты импеданса чаще всего выполняются по следующей формуле:

Z = Um/Im.

Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.

Энергия будет храниться и выделяться в двух типах:

Магнитного поля. Реактивная часть является индуктивной.
Электрического поля.

В чем отличие полярного и неполярного?

Неполярные допускают включение конденсаторов в цепь без учета направления тока. Элементы применяются в фильтрах переменных источников питания, усилителях высокой частоты.

Полярные изделия подсоединяют в соответствии с маркировкой. При включении в обратном направлении прибор выйдет из строя или не будет нормально работать.

Полярные и неполярные конденсаторы большой и малой ёмкости отличаются конструкцией диэлектрика. В электролитических конденсаторах, если оксид наносится на 1 электрод или 1 сторону бумаги, пленки, то элемент будет полярным.

Модели неполярных электролитических конденсаторов, в конструкциях которых оксид металла нанесли симметрично на обе поверхности диэлектрика, включают в цепи с переменным током.

У полярных на корпусе присутствует маркировка положительного или отрицательного электрода.

Энергия устройства

Зарядить конденсатор мгновенно невозможно. Для этого процесса требуется определённое время. Это явление используется в радиотехнике. Так, с помощью конденсатора сглаживаются импульсные всплески. В первом приближении конденсатор похож на аккумулятор. Но при этом он отличается от него принципом накопления энергии, ёмкостью и скоростью заряда разряда. При подключении источника питания к выводам обкладок устройства конденсатор накапливает на них заряд.~

Работу устройства можно объяснить по аналогии с протеканием воды. Пусть имеется сосуд с жидкостью площадью поперечного сечения S. По сути, это эквивалент ёмкости. Тогда вода это будет заряд, а высота водяного столба — напряжение. Получается, что энергия — это произведение зарядов на высоту. Но если аккумулятор можно представить как сосуд, в котором имеется тонкий шланг (вывод) и по которому вытекает вода (заряд), то в конденсаторе его диаметр трубки будет равен размеру всей банки. То есть устройство может мгновенно отдать весь накопленный заряд.

При подаче напряжения на обкладки происходит электризация диэлектрика. В результате происходит смещение и на пластины передаётся энергия. На одной из них возникнет избыток электронов, и она условно зарядится отрицательно, а на второй недостаток — проводник станет положительным. Поэтому в формуле, определяющей заряд на обкладках конденсатора, большое значение имеет диэлектрическая проницаемость непроводящего ток вещества.

Между обкладками возникает сила. Величина действующей со стороны первой равняется F = ε1 * q, а со стороны второй F = ε2 * q. Таким образом, можно записать: F = ε1 * q = ε2 * q = E / 2 * q. При увеличении расстояние между обкладками от нулевого до d, будет выполняться работа: A = F * d. Она направлена на преодоление силы взаимодействия между заряженными проводниками.

То есть: A = E / 2 * q * d. Исходя из того, что ε = U/d будет верно записать: А = 1 / 2 q * U. Значит, механическая работа A в соответствии с законом сохранения энергии будет равна количеству зарядов, запасённых в электрическом поле конденсатора: Wэ = C * U2 / 2.

Следует отметить, что при подаче переменного сигнала внутри диэлектрика происходит постоянная смена знаков заряда. В итоге происходит нагревание, что приводит конденсатор к выходу из строя. Характеризуется это явление тангенсом угла диэлектрических потерь. Определяется он как отношение затраченной мощности к реактивной.