Прямоугольные импульсы: описание и принцип формирования

Электрические импульсы и их параметры

Под электрическим импульсом понимают отклонение напряжения или тока от некоторого постоянного уровня (в частности, от нулевого), наблюдаемое в течение времени, меньшего или сравнимого с длительностью переходных процессов в схеме.

Как уже было сказано, под переходным процессом понимается всякое резкое изменение установившегося режима в электрической цепи за счёт действия внешних сигналов или переключений внутри самой цепи. Таким образом, переходный процесс – это процесс перехода электрической цепи из одного стационарного состояния в другое. Как бы ни был короток этот переходный процесс, – он всегда конечен во времени. Для цепей, в которых время существования переходного процесса несравненно меньше времени действия внешнего сигнала (напряжения или тока), режим работы считается установившимся, а сам внешний сигнал для такой цепи не является импульсным. Примером этого может служить срабатывание электромагнитного реле.

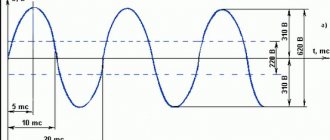
Когда же длительность действующих в электрической цепи сигналов напряжения или тока становится соизмеримой с длительностью процессов установления, переходный процесс оказывает настолько сильное влияние на форму и параметры этих сигналов, что их нельзя не учитывать. В этом случае бóльшая часть времени воздействия сигнала на электрическую цепь совпадает со временем существования переходного процесса (рис.1.4). Режим работы цепи во время действия такого сигнала будет нестационарным, а воздействие его на электрическую цепь – импульсным.

\

а) б)

Рис.1.4. Соотношение между длительностью сигнала и длительностью

переходного процесса:

а) длительность переходного процесса значительно меньше длительности

сигнала (τпп << t);

б) длительность переходного процесса соизмерима с длительностью

сигнала (τпп ≈ t).

Отсюда следует, что понятие импульса связывается с параметрами конкретной цепи и что не для всякой цепи сигнал можно считать импульсным.

Таким образом, электрическим импульсом для данной цепи называется напряжение или ток, действующие в течение промежутка времени, соизмеримого с длительностью переходного процесса в этой цепи.При этом предполагается, что между двумя последовательно действующими в цепи импульсами должен быть достаточный промежуток времени, превышающий длительность процесса установления. В противном случае вместо импульсов будут возникать сигналы сложной формы (рис.1.5).

Рис.1.5. Электрические сигналы сложной формы

Наличие промежутков времени сообщает импульсному сигналу характерную прерывистую структуру. Некоторая условность таких определений заключается в том, что процесс установления теоретически длится бесконечно.

Могут быть такие промежуточные случаи, когда переходные процессы в цепях не успевают практически заканчиваться от импульса к импульсу, хотя действующие сигналы продолжают называть импульсными. В таких случаях возникают дополнительные искажения формы импульсов, вызванные наложением переходного процесса на начало последующего импульса.

Различают два вида импульсов: видеоимпульсы и радиоимпульсы. Видеоимпульсы получают при коммутации (переключении) цепи постоянного тока. Такие импульсы не содержат высокочастотных колебаний и имеют постоянную составляющую (среднее значение), отличную от нуля.

Видеоимпульсы принято различать по их форме. На рис. 1.6. показаны наиболее часто встречающиеся видеоимпульсы.

Рис. 1.6. Формы видеоимпульсов:

а) прямоугольные; б) трапецеидальные; в) остроконечные;

г) пилообразные; д) треугольные; е) разнополярные.

Рассмотрим основные параметры одиночного импульса (рис.1.7).

Рис. 1.7. Параметры одиночного импульса

Форму импульсов и свойства отдельных его участков с количественной стороны оценивают следующими параметрами:

· Um – амплитуда (наибольшее значение) импульса. Амплитуда импульса Um (Im) выражается в вольтах (амперах).

· τ и – длительность импульса. Обычно измерения длительности импульсов или отдельных участков производят на определённом уровне от их основания. Если это не оговаривается, то длительность импульса определяется на нулевом уровне. Однако чаще всего длительность импульса определяется на уровне 0,1Um или 0,5Um, считая от основания. В последнем случае длительность импульса называется активной длительностью и обозначается τ иа. При необходимости и в зависимости от формы импульсов принятые значения уровней для измерения специально оговариваются.

· τф – длительность фронта, определяемая временем нарастания импульса от уровня 0,1Um до уровня 0,9Um .

· τс – длительность среза (заднего фронта), определяемая временем спада импульса от уровня 0,9Um до уровня 0,1Um. Когда длительность фронта или среза измеряется на уровне 0,5Um , она называется активной длительностью и обозначается добавлением индекса «а» аналогично активной длительности импульса. Обычно τф и τссоставляет единицы процентов от длительности импульса. Чем меньше τф и τспо сравнению с τ и, тем больше форма импульса приближается к прямоугольной. Иногда вместо τф и τсфронты импульса характеризуют скоростью нарастания (спада). Эту величину называют крутизной (S) фронта (среза) и выражают в вольтах в секунду (В

/
с) или киловольтах в секунду (кВ
/
с). Для прямоугольного импульса
………………………………(1.14).

· Участок импульса между фронтами называют плоской вершиной. На рис.1.7 показан спад плоской вершины (ΔU).

· Мощность в импульсе. Энергия W импульса, отнесённая к его длительности, определяет мощность в импульсе:

………………………………(1.15).

Она выражается в ваттах (Вт), киловаттах (кВт) или дольных едини-

цах ватта.

В импульсных устройствах используются импульсы, имеющие длительности от долей секунды до наносекунд (10 – 9 с).

Характерными участками импульса (рис.1.8), определяющими его форму,

являются:

· фронт (1 – 2);

· вершина (2 – 3);

· срез (3 – 4), иногда называемый задним фронтом;

· хвост (4 – 5).

Рис.1.8. Характерные участки импульса

Отдельные участки у импульсов различной формы могут отсутствовать. Следует иметь в виду, что реальные импульсы не имеют формы, строго соответствующей названию. Различают импульсы положительной и отрицательной полярности, а также двусторонние (разнополярные) импульсы

(рис. 1.6,е

).

Радиоимпульсами называются импульсы высокочастотных колебаний напряжения или тока обычно синусоидальной формы. Радиоимпульсы не имеют постоянной составляющей. Радиоимпульсы получают модулированием высокочастотных синусоидальных колебаний по амплитуде. При этом амплитудная модуляция производится по закону управляющего видеоимпульса. Формы соответствующих радиоимпульсов, полученных с помощью амплитудной модуляции, показаны на рис. 1.9:

Рис.1.9. Формы радиоимпульсов

Электрические импульсы, следующие друг за другом через равные промежутки времени, называются периодической последовательностью (рис.1.10).

Рис.1.10. Периодическая последовательность импульсов

Периодическая последовательность импульсов характеризуется следующими параметрами:

· Период повторения Тi– промежуток времени между началом двух соседних однополярных импульсов. Он выражается в секундах (с) или дольных единицах секунды (мс; мкс; нс). Величина, обратная периоду повторения, называется частотой повторения (следования) импульсов. Она определяет количество импульсов, в течение одной секунды и выражается в герцах (Гц), килогерцах (кГц) и т.д.

……………………………….. (1.16)

· Скважность последовательности импульсов – это отношение периода повторения к длительности импульса. Обозначается буквой q:

Скважность – безразмерная величина, которая может изменяться в очень широких пределах, так как длительность импульсов может быть в сотни и даже тысячи раз меньше периода импульсов или, наоборот, занимать большую часть периода.

Величина, обратная скважности, называется коэффициентом заполнения. Эта величина безразмерная, меньшая единицы. Она обозначается буквой γ:

…………………………(1.18)

Последовательность импульсов с q = 2 называется «меандром». У такой

последовательности (рис.1.6,е

). Если
Тi>> τи, то такая последовательность называется радиолокационной.
· Среднее значение (постоянная составляющая) импульсного колебания. При определении среднего за период значения импульсного колебания Uср (или Іср) импульс напряжения или тока распределяют равномерно на весь период так, чтобы площадь Uср ·Тiбыла равна площади импульса Sи = Um · τи(рис. 1.10).

Для импульсов любой формы среднее значение определяется из выражения

где U(t) – аналитическое выражение формы импульса.

Для периодической последовательности импульсов прямоугольной формы, у которой U(t) = Um, период повторения Тiи длительность импульса τи, это выражение после подстановки и преобразования принимает вид:

Из рис. 1.10 видно, что Sи = Um · τи= Uср·Тi, откуда следует:

где U0– называется постоянной составляющей.

Таким образом, среднее значение (постоянная составляющая) напряжения (тока) последовательности прямоугольных импульсов в q раз меньше амплитуды импульса.

· Средняя мощность последовательности импульсов. Энергия импульса W, отнесённая к периоду Тi, определяет среднюю мощность импульса

…………………………….. (1.22).

Сравнивая выраженияРии Рср, получим

Ри· τи = Рср· Тi ,

откуда следует

и

т.е. средняя мощность и мощность в импульсе отличаются в q раз.

Отсюда следует, что мощность в импульсе, которую обеспечивает генератор, может в q раз превосходить среднюю мощность генератора.

Задачи и упражнения

1. Амплитуда импульса равна 11 кВ, длительность импульса 1 мкс. Определить крутизну фронта импульса, если считать длительность фронта равной 20 % длительности импульса.

2. Амплитуда прямоугольных импульсов, имеющих частоту следования 1250 Гц и скважность 2300, равна 11 кВ. Определить крутизну фронта и среза, если считать длительность фронта и среза равной 20 % от длительности импульса.

3. Определить постоянную времени цепи, состоящей из конденсатора ёмкостью 5000 пФ и активного сопротивления 0,5 Мом.

4. Определить постоянную времени цепи, состоящей из индуктивности 20 мГн и активного сопротивления 5 кОм.

5. Определить среднюю мощность радиопередающего устройства РЛС, имеющую следующие параметры: импульсная мощность 800 кВт; длительность зондирующего импульса 3,2 мкс; частота следования зондирующих импульсов 375 Гц.

6. Конденсатор ёмкостью 400 пФ заряжается от источника постоянного напряжения 200 В через сопротивление 0,5 Мом. Определить напряжение на конденсаторе через 600 мкс после начала заряда.

7. К цепи, состоящей из конденсатора ёмкостью 10 пФ и сопротивления 2 Мом, подключён источник постоянного тока с напряжением 50 В. Определить ток в момент включения и через 40 мкс после включения.

8. Конденсатор, заряженный до напряжения 300 В, разряжается через сопротивление 300 Мом. Определить величину разрядного тока через время t = 3τ после начала разряда.

9. Какое потребуется время для заряда конденсатора ёмкостью 100 пФ до напряжения 340 В, если напряжение источника 540 В и сопротивление цепи заряда 100 кОм?

10. Цепь, состоящая из индуктивности 10 мГн и сопротивления 5 кОм, подключена к источнику постоянного напряжения 250 В. Определить ток, протекающий в цепи через 4 мкс после включения.

Глава 2. Формирование импульсов

Линейные и нелинейные цепи

В импульсной технике широко применяются цепи и устройства, формирующие напряжения одной формы из напряжения другой. Такие задачи решаются с помощью линейных и нелинейных элементов.

Элемент, параметры которого (сопротивление, индуктивность, ёмкость) не зависят от величины и направления токов и приложенных напряжений, называется линейным.Цепи, содержащие линейные элементы, называются

линейными.

Свойства линейных цепей:

· Вольт-амперная характеристика (ВАХ) линейной цепи представляет собой прямую линию, т.е. величины токов и напряжений будут связаны между собой линейными уравнениями с постоянными коэффициентами. Пример ВАХ такого вида – закон Ома: .

· Для расчёта (анализа) и синтеза линейных цепей применим принцип суперпозиций (наложения). Смысл принципа суперпозиций заключается в следующем: если к входу линейной цепи приложено синусоидальное напряжение, то напряжение на любом её элементе будет иметь такую же форму. Если же входное напряжение является сложным сигналом (т.е. является суммой гармоник), то на любом элементе линейной цепи сохраняются все гармонические составляющие этого сигнала: иначе говоря, сохраняется форма приложенного к входу напряжения. При этом на выходе линейной цепи изменится только соотношение амплитуд гармоник.

· Линейная цепь не преобразует спектр электрического сигнала. Она может изменить составляющие спектра только по амплитуде и фазе. Это является причиной возникновения линейных искажений.

· Всякая реальная линейная цепь искажает форму сигнала за счёт переходных процессов и конечной ширины полосы пропускания.

Строго говоря, все элементы электрических цепей нелинейны. Однако в определённом интервале изменения переменных величин нелинейность элементов проявляется настолько мало, что практически можно пренебречь ею. Примером может служить усилитель радиочастоты (УРЧ) радиоприёмника, на вход которого подаётся очень малый по амплитуде сигнал от антенны.

Нелинейность входной характеристики транзистора, стоящего в первом каскаде УРЧ, в пределах нескольких микровольт настолько мала, что её просто не учитывают.

Обычно область нелинейного поведения элемента ограничена, а переход к нелинейности может происходить либо постепенно, либо скачкообразно.

Если на вход линейной цепи подать сложный сигнал, который является суммой гармоник разных частот, а линейная цепь содержит частотно-зависимый элемент (L или C), то форма напряжений на её элементах не будет повторять форму входного напряжения. Это объясняется тем, что гармоники входного напряжения по-разному пропускаются такой цепью. В результате прохождения входного сигнала через ёмкости и индуктивности цепи соотношения между гармоническими составляющими на элементах цепи изменяются по амплитуде и фазе по отношению к входному сигналу. В результате соотношения между амплитудами и фазами гармоник на входе цепи и на её выходе не одинаковы. Это свойство положено в основу формирования импульсов с помощью линейных цепей.

Элемент, параметры которого зависят от величины и полярности приложенных напряжений или протекающих токов, называется нелинейным, а цепь, содержащую такие элементы, называют нелинейной.

К нелинейным элементам относятся электровакуумные приборы (ЭВП), полупроводниковые приборы (ППП), работающие на нелинейном участке ВАХ, диоды (вакуумные и полупроводниковые), а также трансформаторы с ферромагнетиками.

Свойства нелинейных цепей:

· Ток, протекающий через нелинейный элемент, не пропорционален приложенному к нему напряжению, т.е. зависимость между напряжением и током (ВАХ) носит нелинейный характер. Примером такой ВАХ служат входные и выходные характеристики ЭВП и ППП.

· Процессы, протекающие в нелинейных цепях, описываются нелинейными уравнениями различного вида, коэффициенты которых зависят от самой функции напряжения (тока) или от её производных, а ВАХ нелинейной цепи имеет вид кривой или ломаной линии. Примером могут служить характеристики диодов, триодов, тиристоров, стабилитронов и др.

· Для нелинейных цепей принцип суперпозиций неприменим. При воздействии внешнего сигнала на нелинейные цепи в них всегда возникают токи, содержащие в своём составе новые частотные составляющие, которых не было во входном сигнале. Это является причиной возникновения

нелинейных искажений, в результате чего сигнал на выходе нелинейной

цепи всегда отличается по форме от входного сигнала.

Дифференцирующие цепи

Для того чтобы получить импульс желаемой формы из заданной формы напряжения с помощью пассивной электрической цепи, необходимо знать формирующие свойства этой цепи. Формирующие свойства характеризуют способность линейной цепи определённым образом изменять форму передаваемого (обрабатываемого) сигнала и полностью определяются видом её частотных и временных характеристик.

В импульсной технике для формирования сигналов широко применяются линейные двух- и четырёхполюсники.

Дифференцирующей называется цепь, на выходе которой напряжение пропорционально первой производной от входного напряжения. Математически это выражается следующей формулой:

где Uвх – напряжение на входе дифференцирующей цепи;

Uвых – напряжение на выходе дифференцирующей цепи;

k – коэффициент пропорциональности.

Дифференцирующие цепи (ДЦ) применяются для дифференцирования видеоимпульсов. При этом дифференцирующие цепи позволяют производить следующие преобразования:

· укорочение прямоугольных видеоимпульсов и формирование из них остроконечных импульсов, служащих для запуска и синхронизации различных импульсных устройств;

· получение производных по времени от сложных функций. Это используется в измерительной технике, системах авторегулирования и автосопровождения;

· формирование прямоугольных импульсов из пилообразных.

Простейшими дифференцирующими цепями являются ёмкостная (RC)

и индуктивная (
RL)
цепи (рис.2.1):

а) б)

Рис.2.1. Виды дифференцирующих цепей:

а) ёмкостная ДЦ; б) индуктивная ДЦ

Индуктивная дифференцирующая цепь применяется гораздо реже, чем ёмкостная по чисто практическим соображениям. Дело в том, что для выполнения условия дифференцирования требуется катушка с большой индуктивностью. Такие катушки без железа получаются очень громоздкими и имеют боль-шую паразитную (межвитковую) ёмкость, искажающую результат дифференцирования. Применять же катушки с железом нежелательно, т.к. искажается форма тока из-за нелинейности кривой намагничивания железа, вследствие чего при дифференцировании возникают нелинейные искажения выходного сигнала. Поэтому мы будем рассматривать ёмкостную дифференцирующую цепь.

Покажем, что RC— цепь при определённых условиях становится дифференцирующей.

Известно, что ток, протекающий через ёмкость, определяется выражением:

……………………………………. (2.2).

В то же время из рис.2.1,а

очевидно, что

,

т.к. R и C представляют собой делитель напряжения. Поскольку напряжение

, то .

Выходное напряжение

……………………. (2.3).

Подставив выражение (2.2) в (2.3), получим:

Если выбрать достаточно малую величину R так, чтобы выполнялось условие,

то получим приближённое равенство

Это равенство тождественно (2.1).

Выбрать R достаточно малой величины – это значит обеспечить выполнение неравенства

, т.е. ,

где ωв = 2πfв– верхняя граничная частота гармоники выходного сигнала, ещё имеющая существенное значение для формы выходного импульса.

Коэффициент пропорциональности в выражении (2.1) k = RC = τ носит название постоянной времени дифференцирующей цепи. Чем резче изменяется подводимое напряжение, тем меньшей величиной τ должна обладать дифференцирующая цепь, чтобы на выходе напряжение было близко по форме к производной от Uвх. Параметр τ = RC имеет размерность времени. Это можно подтвердить тем, что в соответствии с Международной системой единиц (СИ) единица измерения электрического сопротивления

а единица измерения электрической ёмкости

Следовательно,

Принцип действия дифференцирующей цепи.

Принципиальная схема ёмкостной дифференцирующей цепи изображена на рис.2.2, а эпюры напряжений – на рис.2.3.

Рис.2.2. Принципиальная схема ёмкостной дифференцирующей цепи

Пусть на вход подаётся идеальный прямоугольный импульс, у которого

τф= τс = 0, а внутреннее сопротивление источника сигнала Ri = 0.Пусть импульс определяется следующим выражением:

1. Исходное состояние схемы (t < t1).

В исходном состоянии Uвх= 0; Uс = 0; iс= 0; Uвых= 0.

1. Первый скачок напряжения (t = t1).

В момент времени t = t1 на вход ДЦ подаётся скачком напряжение

Uвх = Е. В этот момент Uс = 0, т.к. за бесконечно малый промежуток времени ёмкость зарядиться не может. Но, в соответствии с законом коммутации, ток через ёмкость может нарастать мгновенно. Следовательно, в момент t = t1 ток, протекающий через ёмкость, будет равен

Поэтому напряжение на выходе цепи в этот момент будет равно

1. Заряд конденсатора (t1 < t < t2).

После скачка начинается заряд конденсатора током, убывающим по экспоненциальному закону:

Рис.2.3. Эпюры напряжений на элементах дифференцирующей цепи

Напряжение на конденсаторе будет нарастать по экспоненциальному

закону:

Напряжение на выходе ДЦ будет падать по мере нарастания напряжения

заряда на конденсаторе, т.к. R и C представляют собой делитель напряжения:

Необходимо помнить, что в любой момент времени для делителя напряжения выполняется равенство

откуда следует, что

что подтверждает справедливость выражения (2.7).

Теоретически заряд конденсатора будет продолжаться бесконечное время, но практически этот переходный процесс заканчивается через

(3…5)τзар = (3…5)RC.

1. Окончание заряда конденсатора (t = t2).

После окончания переходного процесса ток заряда конденсатора стано-вится равным нулю. Поэтому напряжение на выходе дифференцирующей цепи

достигает практически нулевого значения, т.е. в момент времени t = t2

1. Установившийся режим (t2 < t < t3).

При этом

1. Второй скачок напряжения (t = t3).

В момент времени t = t3 напряжение на входе дифференцирующей цепи скачком падает до нуля. Конденсатор C становится источником напряжения, т.к. он заряжен до величины .

Так как в соответствии с законом коммутации напряжение на конденсаторе скачком изменяться не может, а ток, протекающий через ёмкость, может изменяться скачкообразно, то в момент t = t3 напряжение на выходе скачком уменьшается до – Е. При этом ток разряда в данный момент времени становится максимальным:

а напряжение на выходе дифференцирующей цепи

Выходное напряжение имеет знак «минус», т.к. ток изменил своё направление.

1. Разряд конденсатора (t3 < t < t4).

После второго скачка напряжение на конденсаторе начинает уменьшаться по экспоненциальному закону:

1. Окончание разряда конденсатора и восстановление исходного состояния схемы(t≥ t4).

После окончания переходного процесса разряда конденсатора

Таким образом, схема возвратилась в исходное состояние. Окончание разряда конденсатора наступает практически при t = (3…5)τ = (3…5) RC.

Так как мы приняли внутреннее сопротивление источника сигнала Ri = 0, то можно считать, что постоянные времени цепей заряда и разряда конденсатора τзар = τраз = τ = RC.

В такой идеальной цепи амплитуда выходного напряжения Uвых.mах не зависит от значения параметров цепи R и C, а длительность импульсов на выходе определяется величиной постоянной времени цепи τ = RC. Чем меньше значения R и C, тем быстрее заканчиваются переходные процессы заряда и разряда ёмкости, тем короче импульс на выходе цепи.

Теоретически длительность импульса на выходе дифференцирующей цепи, определяемая по основанию, оказывается бесконечно большой, поскольку напряжение на выходе спадает экспоненциально. Поэтому длительность импульса определяется на определённом уровне от основания

U0 = αUвых(рис.2.4):

Рис.2.4. Определение длительности импульса на уровне U0 после

дифференцирования

Определим длительность продифференцированного импульса на уровне

U0 = αUвых:

………………. (2.8),

откуда и

Дифференцирование всегда сопровождается укорочением длительности импульса. Это означает, что ёмкость C должна успевать полностью зарядиться за время действующего входного дифференцируемого импульса. Следовательно, условием практического дифференцирования с целью укорочения длительности импульса является соотношение:

τи вх > 5τ = 5RC.

Чем меньше τ цепи, тем быстрее заряжается и разряжается конденсатор и тем меньшую длительность имеют выходные импульсы, тем более остроконечными они становятся и, следовательно, тем точнее дифференцирование. Однако уменьшать τ целесообразно до определённого предела.

Изменение формы импульса на выходе дифференцирующей цепи можно объяснить с точки зрения спектрального анализа.

Каждая гармоника входного импульса делится между R и C. Для гармоник низких частот, определяющих вершину входного импульса, конденсатор представляет большое сопротивление, т.к.

>> R.

Поэтому на выход плоская вершина входного импульса почти не передаётся.

Для высокочастотных составляющих входного импульса, формирующих его фронт и срез,

<< R.

Поэтому фронт и срез входного импульса на выход передаются практически без ослабления. Эти соображения позволяют определить дифференцирующую цепь как фильтр верхних частот.

Переходный процесс

Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т.д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.

Исходя из вышесказанного, можно сделать вывод, что напряжение на ёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.

Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей). Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.

Влияние RC- и RL-цепей на импульсы различной формы

Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.

Ступенчатое изменение напряжения

. При подключении RC-цепи к источнику постоянного напряжения uвх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:

где е – математическая постоянная, е = 2,72; t – время, с; τ

– постоянная времени, с.
τ = RC
.

С определением напряжения всё понятно, но в практике чаще возникает вопрос о времени установления напряжения. Например, необходимо вычислить время за которое на конденсаторе установится напряжение равное uС = 0,95 Е. Простым преобразованием формулы напряжения получим

Аналогично при подключении RL-цепи к источнику постоянного напряжения uвх = Е = const

где τ

– постоянная времени, с.
τ = L/R
.

Линейно изменяющееся напряжение

. При подключении RC-цепи к источнику линейно изменяющегося напряжения uВХ = kt, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

Для RL-цепи подключённой к источнику с линейно изменяющимся напряжением uВХ = kt, напряжения на элементах соответственно будут такими

Экспоненциально изменяющееся напряжение. При подключении RC-цепи к источнику экспоненциально изменяющегося напряжения , напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

где q = τ/τ1.

Соответственно напряжение на конденсаторе будет равно разности напряжений источника и напряжения на резисторе

Временные диаграммы для uR представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений uR близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения uR, уменьшается и максимальное значение uR.

Временные диаграммы напряжений на резисторе RC-цепи при различных значениях q = τ/τ1.

Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.