Что такое фильтр нижних частот? Руководство по основам пассивных RC фильтров

Временная область и частотная область

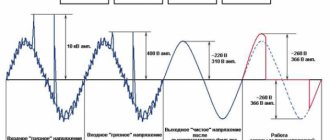
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения относительно времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. На осциллографе вы видите представление сигнала во временной области.

Типовая осциллограмма проста и интуитивно понятна, но она также имеет некоторые ограничения, поскольку она напрямую не раскрывает частотный состав сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром) передает информацию о сигнале посредством определения различных частотных компонентов, которые представлены одновременно.

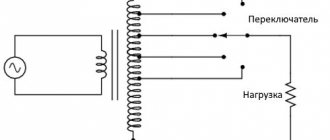
Классификация по топологии

Электронные фильтры можно классифицировать по технологии их реализации. пассивный фильтр и активный фильтр технологии можно дополнительно классифицировать по конкретным топология электронного фильтра используется для их реализации.

Любая заданная передаточная функция фильтра может быть реализована в любом топология электронного фильтра.

Вот некоторые распространенные топологии схем:

• Топология Кауэра — пассивный
• Топология Саллена – Ки — активный
• Топология множественной обратной связи — активный
• Топология переменной состояния — активный
• Биквадратичная топология — активный

Что такое фильтр?

Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.

Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.

Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.

Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.

Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.

История

Основная статья: Аналоговый фильтр

Первыми электронными фильтрами были аналоговые пассивные линейные фильтры, построенные только с резисторами и конденсаторами или резисторами и индукторами . Эти фильтры известны как однополюсные RC RL соответственно . Эти типы простых фильтров имеют очень ограниченное применение. Многополюсные — фильтры , представленные в 1910 году, позволяют лучше контролировать реакцию сигнала.

Позже появились гибридные фильтры, которые обычно состоят из комбинации аналоговых усилителей с механическими резонансными линиями или линиями задержки. Другие устройства, такие как CCD (устройства с зарядовой связью) с аналоговыми линиями задержки, также используются в качестве фильтров дискретного времени.

Наконец, с появлением цифровых технологий и цифровой обработки данных были созданы очень популярные сегодня цифровые активные фильтры.

Типы фильтров

В зависимости от особенностей амплитудно-частотных характеристик фильтры можно распределить по широким категориям. Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр верхних частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и режекторные фильтры, которые блокируют только относительно узкий диапазон частот.

Фильтры также могут быть классифицированы в соответствии с типами компонентов, которые используются для реализации схемы. Пассивные фильтры используют резисторы, конденсаторы и катушки индуктивности; эти компоненты не способны обеспечить усиление, и, следовательно, пассивный фильтр может только сохранять или уменьшать амплитуду входного сигнала. Активный фильтр, напротив, может фильтровать сигнал и применять усиление, поскольку он включает в себя активный компонент, такой как транзистор или операционный усилитель.

В данной статье рассматривается анализ и проектирование пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.

Г-образные фильтры

Г-образные фильтры состоят из двух радиоэлементов, один или два из которых имеют нелинейную АЧХ.

RC-фильтры

Думаю, начнем с самого известного нам фильтра, состоящего из резистора и конденсатора. Он имеет две модификации:

С первого взгляда можно подумать, что это два одинаковых фильтра, но это не так. В этом легко убедиться, если построить АЧХ для каждого фильтра.

В этом деле нам поможет Proteus. Итак, АЧХ для этой цепи

будет выглядеть вот так:

Как мы видим, АЧХ такого фильтра беспрепятственно пропускает низкие частоты, а с ростом частоты ослабляет высокие частоты. Поэтому, такой фильтр называют фильтром низких частот (ФНЧ).

А вот для этой цепи

АЧХ будет выглядеть таким образом

Здесь как раз все наоборот. Такой фильтр ослабляет низкие частоты и пропускает высокие частоты, поэтому такой фильтр называется фильтром высокой частоты (ФВЧ).

Наклон характеристики АЧХ

Наклон АЧХ в обоих случаях равняется 6 дБ/октаву после точки, соответствующей значению коэффициента передачи в -3дБ, то есть частоты среза. Что означает запись 6 дБ/октаву? До или после частоты среза, наклон АЧХ принимает вид почти прямой линии при условии, что коэффициент передачи измеряем в . Октава — это соотношение частот два к одному. В нашем примере наклон АЧХ в 6 дБ/октаву говорит о том, что при увеличении частоты в два раза, у нас прямая АЧХ растет (или падает) на 6 дБ.

Давайте рассмотрим этот пример

Возьмем частоту 1 КГц. На частоте от 1 КГц до 2 КГц падение АЧХ составит 6 дБ. На промежутке от 2 КГц и до 4 КГц АЧХ снова падает на 6 дБ, на промежутке от 4 КГц и до 8 КГц снова падает на 6 дБ, на частоте от 8 КГц и до 16 КГц затухание АЧХ снова будет 6 дБ и тд. , следовательно, наклон АЧХ составляет 6 дБ/октаву. Есть также такое понятие, как дБ/декада. Оно используется реже и обозначает разницу между частотами в 10 раз. Как найти /декаду можно прочитать в этой статье.

Чем больше крутизна наклона прямой АЧХ, тем лучше избирательные свойства фильтра:

Фильтр, с характеристикой наклона в 24 дБ/октаву явно будет лучше, чем в 6 дБ/октаву, так как становится более приближенным к идеальному.

RL-фильтры

Почему бы не заменить конденсатор катушкой индуктивности? Получаем снова два типа фильтров:

Для этого фильтра

АЧХ принимает такой вид:

Получили все тот же самый ФНЧ

а для такой цепи

АЧХ примет такой вид

Тот же самый фильтр ФВЧ

RC и RL фильтры называют фильтрами первого порядка и они обеспечивают наклон характеристики АЧХ в 6 дБ/октаву после частоты среза.

LC-фильтры

А что если заменить резистор конденсатором? Итого мы имеем в схеме два радиоэлемента, реактивное сопротивление которых зависит от частоты. Здесь получаются также два варианта:

Давайте рассмотрим АЧХ этого фильтра

Как вы могли заметить, его АЧХ в области низких частот получилась наиболее плоской и заканчивается шипом. Откуда вообще он взялся? Мало того, что цепь собрана из пассивных радиоэлементов, так она еще и усиливает сигнал по напряжению в области шипа!? Но не стоит радоваться. Усиливает по напряжению, а не по мощности. Дело в том, что мы получили последовательный колебательный контур, у которого, как вы помните, на частоте резонанса возникает резонанс напряжений. При резонансе напряжений, напряжение на катушке равняется напряжению на конденсаторе.

Но это еще не все. Это напряжение в Q раз больше, чем напряжение, подаваемое на последовательный колебательный контур. А что такое Q? Это добротность. Вас этот шип не должен смущать, так как высота пика зависит от добротности, которая в реальных схемах составляет небольшое значение. Примечательна эта схема также тем, что наклон ее характеристики составляет 12 дБ/октаву, что в два раза лучше, чем у RC и RL фильтров. Кстати, если даже максимальная амплитуда превышает значения в 0 дБ, то все равно полосу пропускания определяем на уровне в -3 дБ. Об этом тоже не стоит забывать.

Все то же самое касается и ФВЧ фильтра

Как я уже сказал, LC фильтры называют уже фильтрами второго порядка и они обеспечивают наклон АЧХ в 12 дБ/октаву.

RC фильтр нижних частот

Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, которая состоит из резистора и либо конденсатора, либо катушки индуктивности. Теоретически, топология фильтров нижних частот резистор-индуктивность (RL) эквивалентна, с точки зрения фильтрующей способности, топологии фильтров нижних частот резистор-конденсатор (RC). Однако на практике версия резистор-конденсатор встречается гораздо чаще, и, следовательно, оставшаяся часть этой статьи будет посвящена RC фильтру нижних частот.

Как вы можете видеть на схеме, пропускающая нижние частоты частотная характеристика RC фильтра создается путем установки резистора последовательно с путем прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка является отдельным компонентом, но в реальной цепи она может представлять что-то гораздо более сложное, например, аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения амплитудно-частотной характеристики фильтра.

Мы можем интуитивно проанализировать фильтрующее действие топологии RC фильтра нижних частот, если поймем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.

Когда частота входного сигнала низкая, полное сопротивление конденсатора будет высоким относительно полного сопротивления резистора; таким образом, большая часть входного напряжения падает на конденсаторе (и на нагрузке, которая параллельна конденсатору). Когда входная частота высокая, полное сопротивление конденсатора будет низким по сравнению с полным сопротивлением резистора, что означает, что на резисторе падает большее напряжение, и меньшее напряжение передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.

Это качественное объяснение работы RC фильтра нижних частот является важным первым шагом, но оно не очень полезно, когда нам нужно проектировать реальную схему, потому что термины «высокая частота» и «низкая частота» чрезвычайно расплывчаты. Инженеры должны создавать схемы, которые пропускают и блокируют определенные частоты. Например, в аудиосистеме, описанной выше, мы хотим сохранить сигнал 5 кГц и подавить сигнал 500 кГц. Это означает, что нам нужен фильтр, который переходит от пропускания к блокировке где-то между 5 кГц и 500 кГц.

Полосовые фильтры

В прошлой статье мы с вами рассматривали один из примеров полосового фильтра

Вот так выглядит АЧХ этого фильтра.

Особенность таких фильтров такова, что они имеют две частоты среза. Определяются они также на уровне в -3дБ или на уровне в 0,707 от максимального значения коэффициента передачи, а еще точнее Ku max/√2.

Полосовые резонансные фильтры

Если нам надо выделить какую-то узкую полосу частот, для этого применяются LC-резонанcные фильтры. Еще их часто называют избирательными. Давайте рассмотрим одного из их представителя.

LC-контур в сочетании с резистором R образует делитель напряжения. Катушка и конденсатор в паре создают параллельный колебательный контур, который на частоте резонанса будет иметь очень высокий импеданс, в народе — обрыв цепи. В результате, на выходе цепи при резонансе будет значение входного напряжения, при условии если мы к выходу такого фильтра не цепляем никакой нагрузки.

АЧХ данного фильтра будет выглядеть примерно вот так:

В реальной же цепи пик характеристики АЧХ будет сглажен за счет потерь в катушке и конденсаторе, так как катушка и конденсатор обладают паразитными параметрами.

Если взять по оси Y значение коэффициента передачи, то график АЧХ будет выглядеть следующим образом:

Постройте прямую на уровне в 0,707 и оцените полосу пропускания такого фильтра. Как вы можете заметить, она будет очень узкой. Коэффициент добротности Q позволяет оценить характеристику контура. Чем большее добротность, тем острее характеристика.

Как же определить добротность из графика? Для этого надо найти резонансную частоту по формуле:

где

f0— это резонансная частота контура, Гц

L — индуктивность катушки, Гн

С — емкость конденсатора, Ф

Подставляем L=1mH и С=1uF и получаем для нашего контура резонансную частоту в 5033 Гц.

Теперь надо определить полосу пропускания нашего фильтра. Делается это как обычно на уровне в -3 дБ, если вертикальная шкала в децибелах, либо на уровне в 0,707, если шкала линейная.

Давайте увеличим верхушку нашей АЧХ и найдем две частоты среза.

f1 = 4839 Гц

f2 = 5233 Гц

Следовательно, полоса пропускания Δf=f2 — f1 = 5233-4839=394 Гц

Ну и осталось найти добротность:

Q=5033/394=12,77

Режекторные фильтры

Другой разновидностью LC схем является последовательная LC-схема.

Ее АЧХ будет выглядеть примерно вот так:

Как можно увидеть, такая схема на резонансной частоте и вблизи нее как бы вырезает небольшой диапазон частот. Здесь вступает в силу резонанс последовательного колебательного контура. Как вы помните, на резонансной частоте сопротивление контура будет равняться его активному сопротивлению. Активное сопротивление контура составляют паразитные параметры катушки и конденсатора, поэтому падение напряжения на самом контуре будет равняться падению напряжения на паразитном сопротивлении, которое очень мало. Такой фильтр называют узкополосным режекторным фильтром.

Индуктивность катушки. Формула есть по ссылке.

На практике звенья таких фильтров каскадируют, чтобы получить различные фильтры с требуемой полосой пропускания. Но есть один минус у фильтров, в которых имеется катушка индуктивности. Катушки дорогие, громоздкие, имеют много паразитных параметров. Они чувствительны к фону, который магнитным путем наводится от расположенных поблизости силовых трансформаторов.

Конечно, этот недостаток можно устранить, поместив катушку индуктивности в экран из мю-металла, но от этого она станет только дороже. Проектировщики всячески пытаются избежать катушек индуктивности, если это возможно. Но, благодаря прогрессу, в настоящее время катушки не используются в активных фильтрах, построенных на ОУ.

Видео на тему «Как работает электрический фильтр», рекомендую к просмотру:

Частота среза

Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.

Когда вы посмотрите на график амплитудно-частотной характеристики RC фильтра, вы заметите, что термин «частота среза» не очень точен. Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание увеличивается постепенно по мере того, как частоты перемещаются от значений ниже частоты среза к значениям выше частоты среза.

Частота среза RC фильтра нижних частот фактически является частотой, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, поскольку уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частоту среза также называют частотой -3 дБ, и на самом деле это название является более точным и более информативным. Термин полоса пропускания относится к ширине полосы пропускания фильтра, и в случае фильтра нижних частот полоса пропускания равна частоте -3 дБ (как показано на диаграмме ниже).

Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:

\[f_{ср} = \frac{1}{2\pi RC}\]

Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.

\[100 \times 10^3 = \frac{1}{2 \pi R (10\times 10^{-9})} \\ \Rightarrow R=\frac{1}{2 \pi (10\times 10^{-9})(100 \times 10^3)} = 159,15 \ Ом\]

Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.

внешняя ссылка

• библиотека для создания цифровых фильтров с помощью LabVIEW
• библиотека для построения адаптивных фильтров с помощью LabVIEW
• Основы электротехники и электроники
• Аналоговые фильтры для преобразования данных
• Некоторые интересные конфигурации и преобразования дизайна фильтров

• Данные: Q327754
• Мультимедиа: электронные фильтры

Расчет амплитудно-частотной характеристики фильтра

Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:

Рисунок 9 – Резистивный делитель напряжения

\[V_{вых} = V_{вх} \left( \frac{R_2}{R_1 + R_2} \right)\]

RC фильтр использует эквивалентную структуру, но вместо R2 у нас конденсатор. Сначала мы заменим R2 (в числителе) на реактивное сопротивление конденсатора (XC). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем

\[V_{вых} = V_{вх} \left( \frac{X_C}{\sqrt{R_1^2+X_C^2}} \right)\]

Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:

\[X_C=\frac{1}{2 \pi f C}\]

В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда Vвх равна 1 В, поэтому мы можем просто удалить Vвх из расчетов. Сначала давайте рассчитаем амплитуду Vвых на частоте необходимой нам синусоиды:

\[X_{C\_5кГц} = \frac{1}{2 \pi (5000)(10 \times 10^{-9})}= 3183\ Ом\]

\[V_{вых\_5кГц} = \frac{3183}{\sqrt{3183^2+160^2}}= 0,999 \ В\]

Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).

Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.

\[X_{C\_500кГц} = \frac{1}{2 \pi (500 \times 10^3)(10 \times 10^{-9})}= 31,8\ Ом\]

\[V_{вых\_500кГц} = \frac{31,8}{\sqrt{31,8^2+160^2}}= 0,195 \ В\]

Амплитуда шума составляет всего около 20% от первоначального значения.

Визуализация амплитудно-частотной характеристики фильтра

Наиболее удобным способом оценки влияния фильтра на сигнал является изучение графика его амплитудно-частотной характеристики. На этих графиках, часто называемых графиками Боде, амплитуда (в децибелах) откладывается по вертикальной оси, а частота – по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, поэтому физическое расстояние между 1 Гц и 10 Гц такое же, как физическое расстояние между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Такая конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень широком диапазоне частот.

Каждая точка на кривой указывает амплитуду, которую будет иметь выходной сигнал, если входной сигнал имеет величину 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда частота входного сигнала равна 1 МГц, амплитуда выходного сигнала (при условии, что амплитуда входного сигнала равна 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).

Общий вид этой кривой амплитудно-частотной характеристики станет вам очень знакомым, если вы будете проводить больше времени со схемами фильтров. Кривая почти идеально плоская в полосе пропускания, а затем, по мере приближения частоты входного сигнала к частоте среза, скорость ее спада начинает увеличиваться. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ/декада, то есть уровень выходного сигнала уменьшается на 20 дБ при каждом увеличении частоты входного сигнала в десять раз.

Оценка производительности фильтра нижних частот

Если мы построим амплитудно-частотную характеристику фильтра, который мы разработали ранее в этой статье, то увидим, что амплитудный отклик на 5 кГц, по сути, равен 0 дБ (т.е. почти нулевое затухание), а амплитудный отклик на 500 кГц составляет приблизительно –14 дБ (что соответствует коэффициенту передачи 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.

Поскольку RC фильтры всегда имеют плавный переход от полосы пропускания к полосе задерживания, а затухание никогда не достигает бесконечности, мы не можем разработать «идеальный» фильтр, то есть фильтр, который не влияет на необходимый синусоидальный сигнал и полностью устраняет шум. Вместо этого у нас всегда есть компромисс. Если мы сместим частоту среза ближе к 5 кГц, то получим большее затухание шума, но так же и большее затухание полезного синусоидального сигнала, который мы хотим отправить на динамик. Если мы переместим частоту среза ближе к 500 кГц, то получим меньшее затухание на частоте полезного сигнала, но так же и меньшее затухание на частоте шума.

Функция передачи

Независимо от конкретной реализации фильтра, за исключением того, что он должен быть линейным ( аналоговым , цифровым или механическим), его поведение описывается его передаточной функцией . Это определяет, как приложенный сигнал изменяется по амплитуде и фазе для каждой частоты при прохождении через фильтр. Выбранная передаточная функция типична для фильтра. Вот некоторые распространенные фильтры:

• Фильтр Баттерворта с гладкой полосой пропускания и резким срезом.
• Фильтр Чебышева , с резким срезом, но с волнистой полосой пропускания
• Эллиптические фильтры или фильтр Кауэра , которые достигают более резкой переходной зоны, чем предыдущие, за счет колебаний во всех ее полосах.
• Фильтр Бесселя , который, будучи аналоговым, обеспечивает постоянное изменение фазы

Передаточную функцию можно математически выразить в виде дроби с помощью соответствующих частотных преобразований. Говорят, что значения, которые делают числитель нулевым, являются нулями, а те, которые делают нулевой знаменатель, являются полюсами.

ЧАС ( ж ) знак равно п ты м е р а d В р ( ж ) d е п В м я п а d В р ( ж ) {\ Displaystyle Н (е) = {\ гидроразрыва {numerador (f)} {denominador (f)}}}

Количество полюсов и нулей указывает порядок фильтра, а его значение определяет характеристики фильтра, такие как его частотная характеристика и стабильность.

Фазовый сдвиг фильтра низких частот

До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных составляющих в сигнале. Однако реактивные элементы цепи в дополнение к влиянию на амплитуду всегда вносят сдвиг фазы.

Понятие фазы относится к значению периодического сигнала в определенный момент цикла. Таким образом, когда мы говорим, что схема вызывает сдвиг фазы, то имеем в виду, что она создает смещение между входным и выходным сигналами: входной и выходной сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение сдвига фазы, например, 45° или 90°, показывает, какое было создано смещение.

Каждый реактивный элемент в цепи вводит сдвиг фазы на 90°, но этот фазовый сдвиг происходит не сразу. Фаза выходного сигнала, так же как и амплитуда выходного сигнала, изменяется постепенно по мере увеличения частоты входного сигнала. В RC фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге будет вводить сдвиг фазы на 90°.

Как и в случае амплитудно-частотной характеристикой, фазо-частотную характеристику легче всего оценить, изучив график, на котором частота на горизонтальной оси приведена в логарифмическом масштабе. Приведенное ниже описание дает общее представление, а затем вы можете заполнить детали, изучив график.

• Сдвиг фазы изначально равен 0°.
• Он постепенно увеличивается до достижения 45° на частоте среза; на этом участке характеристики скорость изменения увеличивается.
• После частоты среза сдвиг фазы продолжает увеличиваться, но скорость изменения уменьшается.
• Скорость изменения становится очень малой, когда сдвиг фазы асимптотически приближается к 90 °.

Что надо знать при выборе сетевого фильтра

При выборе любого промежуточного сетевого устройства – удлинителя, сетевого фильтра, стабилизатора или источника бесперебойного питания, прежде всего следует помнить главное правило: «электротехника – наука о контактах». Красивые надписи, громкие имена брендов, многочисленные индикаторы и USB-порты не должны отвлекать от главной проблемы: включая что-либо между сетью и устройством, мы добавляем лишние контакты в и без того длинную и неравномерную цепь.

• Даже самые совершенные схемотехнические решения для стабилизации, фильтрации и защиты попросту бессмысленны, если контакты в розетках вырезаны из консервной банки и болтаются по чем зря, а пайка разъемов сделана некачественно. В таких условиях любые перепады нагрузки в сети будут автоматически создавать многочисленные помехи.

• Просчитайте заранее количество необходимых розеток для подключения техники, чтобы впоследствии не пришлось городить огород ненужных дополнительных контактов из удлинителей и других переходников.
  Хороший сетевой фильтр или стабилизатор может обладать индикацией наличия заземления или режима перегрузки, это полезный бонус. Что касается встроенного в сетевой фильтр зарядного устройства с одним или несколькими портами USB – это, скорее, приятная мелочь, несколько влияющая на цену, но никак не связанная с основной функцией устройства.

• В процессе выбора сетевого фильтра важно обратить внимание на суммарную энергию пиковых выбросов паразитного напряжения (в джоулях), которую устройство теоретически в состоянии отфильтровать и погасить в каждый момент времени без саморазрушения. Впрочем, максимальное число джоулей в спецификации фильтра – тоже не истина в последней инстанции, поскольку правильно спроектированный фильтр способен «заземлять» часть энергии через варисторы. Тем не менее, в процессе выбора маркировку фильтра в джоулях не стоит сбрасывать со счетов.

• Следующий важный параметр – максимальный ток помехи, на который рассчитан фильтр, в амперах. В дополнение, сетевой фильтр также может быть промаркирован по максимальной нагрузке, при этом она может быть указана как в амперах, так и в ваттах.

• Некоторые производители также добавляют в список характеристик сетевых фильтров максимально допустимое напряжение (в вольтах) уровень ослабления высокочастотных помех для разных частот (в децибелах) и наличие защиты от перегрузки – например, от перегрева. Наконец, ряд параметров фильтра, определяющий его выбор в каждом отдельном случае: длина кабеля, количество розеток, возможность настенного монтажа, наличие дополнительных фильтров для телефонной линии и витой пары, наличие портов USB и так далее.

Фильтры нижних частот второго порядка

До сих пор мы предполагали, что RC фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация является фильтром первого порядка.

«Порядок» пассивного фильтра определяется количеством реактивных элементов, то есть конденсаторов или индуктивностей, которые присутствуют в цепи. Фильтр более высокого порядка имеет больше реактивных элементов, что приводит к большему сдвигу фазы и более крутому спаду АЧХ. Эта вторая характеристика является основной причиной для увеличения порядка фильтра.

Добавляя один реактивный элемент к фильтру, например, переходя от первого порядка ко второму или от второго к третьему, мы увеличиваем максимальный спад на 20 дБ/декада. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому затуханию, и это может привести к улучшению производительности, когда нет широкой полосы частот, отделяющей необходимые частотные компоненты от шумовых компонентов.

Фильтры второго порядка обычно строятся вокруг резонансного контура, состоящего из катушки индуктивности и конденсатора (эта топология называется «RLC», т.е. резистор-индуктивность-конденсатор). Однако также возможно создание RC фильтров второго порядка. Как показано на рисунке ниже, всё, что нам нужно сделать, это включить каскадно два RC фильтра первого порядка.

Хотя эта топология, безусловно, создает характеристику второго порядка, она широко не используется – как мы увидим в следующем разделе, ее амплитудно-частотная характеристика часто уступает амплитудно-частотной характеристике активного фильтра второго порядка или RLC фильтра второго порядка.

Фильтры электросетей

Помимо указанных выше в любой аппаратуре устанавливаются фильтры цепей питания. Их задача пропускать внутрь лишь напряжение частотой 50 Гц, остальное отсеивать. Техника, выпускаемая в СССР, не способна была похвастаться качественной фильтрацией, требования были иные. Сегодня чуткая электроника легко выходит из строя от статической и обычной помехи. Наводки легко сжигали графические адаптеры первых компьютеров.

Постепенно электроника стала более защищённой, но сетевой фильтр входит в состав любого оборудования, где содержатся микросхемы. Это не совсем правильно, работающие двигатели любого типа создают много помех:

• Асинхронные создают большие скачки напряжения при старте и пуске. В процессе работы влияние на питающую цепь не столь велико.
• Коллекторные постоянно засоряют линию питания помехой из-за искрения. Работающий пылесос сильно мешает соседям.

Фильтры регулирующей и защитной аппаратуры

Помимо электрических фильтров цепей питания бытовой аппаратуры своеобразное оборудование со схожими задачами встречается в промышленности. Речь сейчас идёт о регулировании. В процессе эксплуатации двигателей создаются помехи, специальные фильтры занимаются указанной ситуацией, но отдельной строкой идёт эффективность. Подразумевается фактор мощности и реактивная составляющая.

Когда работает двигатель, случается порой, что энергия отдаётся обратно в сеть. К примеру, при динамическом торможении вал кратковременно входит в зону генерации, цепь питания получает скачок напряжения. Но и в номинальных режимах развивается процесс возвращения мощности.

Трансформаторы подстанций формируют напряжение не для возврата. Наличие реактивных сопротивлений в цепи приводит к подобному. Образуется нечто вроде колебательного контура, по которому энергия без дела снуёт туда и сюда. Разогревает провода, не выполняя полезной работы. Это давно замечено, порой предприятие штрафуется. Энергетики требуют установки счётчиков реактивной (возвращаемой) мощности.

Для анализа промышленных цепей в 1918 году разработан метод симметричных составляющих. Оказалось, что потребляемый ток представляется в виде трёх компонентов:

1. Прямая последовательность.
2. Обратная последовательность.
3. Нулевая последовательность.

В литературе, в особенности современной, нет чёткого описания значения выражений. Намеренное внесение путаницы только отупляет читателей. В действительности названия чётко определяют предмет разговора, точно отражая суть. Прямая последовательность присутствует при чисто активной мощности, когда энергия назад не отражается, а нулевая показывает, текут ли токи в цепи нейтрали. Последнее случается при авариях, несимметричной нагрузке. Обратная по смыслу характеризует реактивную мощность и возникает в идентичных условиях.

Симметричные составляющие

Из-за наличия реактивных сопротивлений по линиям трёхфазного тока напряжение несимметричное. Оно отклонено от номинала на некоторый угол на векторной диаграмме. В результате становится сложным провести анализ. Ток течёт одновременно для питания оборудования и обратно – отражённый реактивной частью сопротивления.

Придуман анализ методом симметричных составляющих. Где каждый сигнал раскладывается на последовательности, как указано выше. Любое несимметричное напряжение или ток представляется в виде суммы трёх симметричных составляющих. Каждая характеризовать конкретный процесс. К примеру, прямая последовательность характеризует потребляемую мощность. Векторное сложение всех трёх даёт напряжение или ток в фазе, в которой они текут по цепи.

В прямой последовательности векторы сдвинуты в соседних линиях на 120 градусов, формируя питающий трансформатор. В обратной – аналогично, но порядок фаз обратный. Если брать прямой порядок, сдвиг фаз составляет 240 градусов. Это причина названия обратной последовательности. Третий ряд векторов принципиально отличается от двух прочих. В нем сдвиг фаз между напряжениями или токами равен нулю. Они вращаются синхронно.

Для проведения указанных математических операций созданы специальные формулы. Результат разложения несимметричной последовательности – на рисунке. Поскольку метод искусственный, нельзя видеть составляющие при помощи обычных амперметров и вольтметров. Исключениями служат идеальные случаи:

1. В идеально симметричных режимах потребления по всем фазам или аналогичного рода коротких замыканиях видим на осциллографе прямую последовательность.
2. Обратная последовательность отмечается в случае короткого замыкания по одной либо двум фазам. Либо в случае выраженной асимметрии потребления.
3. Аналогичное говорится про нулевую последовательность. При коротких замыканиях между фазами подобная составляющая отсутствует. И ярко проявляется исключительно при утечках на грунт.

Итак, любая трёхфазная сеть представляется тремя вымышленными, где текут по отдельности перечисленные последовательности. И значения токов и напряжений тогда допустимо использовать для регулирования и защиты. Чтобы реализовать это на практике, применяют фильтры-реле симметричных последовательностей.

Фильтры симметричных составляющих

Фильтры симметричных составляющих работают с напряжением или током и подключаются через соответствующие трансформаторы. На вход указанных устройств поступают входные снимаемые величины, на выходе образуется управляющий сигнал. Напряжение обычно отбирается по схеме звезды, требуется получить информацию по каждой линии в отдельности.

Фильтры последовательностей считаются специфическим оборудованием и называются так за то, что при отсутствии целевого сигнала не выдают управляющих воздействий. Даже если на входе присутствуют параметры. Выходит, выполняют фильтрующую функцию. Отсюда проистекает требование наличия трёх типов. К примеру, фильтры прямой последовательности используют для учёта активной энергии. Но в большинстве случаев оборудование становится частью оснастки крупных предприятий.

Встречаются комбинированные фильтры. Все виды коротких замыканий не отслеживаются по одному типу последовательности. Фильтры симметричных последовательностей включают в состав реле, не способные работать с обычными, выпускаемыми серийно. При попытке подогнать их нагрузочную характеристику сильно возрастает объем, увеличивается масса. В этом секрет странного названия – фильтр-реле.

Дополнительной особенностью становится отсутствие единого корпуса. Составляющие фильтра расположены отдельно в силу наличия разнородных устройств в составе: трансформаторов, дросселей, ёмкостей, резисторов и пр. Помимо тока и напряжения эти устройства способны отслеживать и мощность. В последнем случае становится возможным реализация на их основе счётчиков. Но, как говорилось выше, электрические фильтры-реле гораздо чаще применяются в цепях защиты.

Амплитудно-частотная характеристика RC фильтра второго порядка

Мы можем попытаться создать RC фильтр нижних частот второго порядка, разработав фильтр первого порядка в соответствии с необходимой частотой среза, а затем соединив два этих каскада первого порядка последовательно. Это даст фильтр, который имеет аналогичную общую амплитудно-частотную характеристику и максимальный спад 40 дБ/декада вместо 20 дБ/декада.

Однако если мы посмотрим на АЧХ более внимательно, то увидим, что частота –3 дБ снизилась. RC фильтр второго порядка ведет себя не так, как ожидалось, поскольку эти два звена не являются независимыми – мы не можем просто соединить эти две звена вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка.

Кроме того, даже если мы вставим буфер между этими двумя звеньями, чтобы первое RC звено и второе RC звено могли работать как независимые фильтры, затухание на исходной частоте среза будет составлять 6 дБ вместо 3 дБ. Это происходит именно потому, что два звена работают независимо – первый фильтр вносит затухание 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ затухания.

Основное ограничение RC фильтра нижних частот второго порядка состоит в том, что разработчик не может точно настроить переход от полосы пропускания к полосе задерживания, регулируя добротность (Q) фильтра; этот параметр указывает, насколько сглажена амплитудно-частотная характеристика. Если вы каскадно соединяете два идентичных RC фильтра нижних частот, общая передаточная функция соответствует отклику второго порядка, но добротность всегда равна 0,5. Когда Q = 0,5, фильтр находится на границе чрезмерного затухания, и это приводит к амплитудно-частотной характеристике, которая «провисает» в переходной области. Активные фильтры второго порядка и резонансные фильтры второго порядка не имеют такого ограничения; разработчик может управлять добротностью и, таким образом, точно настраивать амплитудно-частотную характеристику в переходной области.

Сложные фильтры

Что будет, если соединить два фильтра первого порядка друг за другом? Как ни странно, получится фильтр второго порядка.

Его АЧХ будет более крутой, а именно 12 дБ/октаву, что характерно для фильтров второго порядка. Догадайтесь, какой наклон будет у фильтра третьего порядка ? Все верно, прибавляем 6 дБ/октаву и получаем 18 дБ/октаву. Соответственно, у фильтра 4 -ого порядка наклон АЧХ будет уже 24 дБ/октаву и тд. То есть, чем больше звеньев мы соединим, тем круче будет наклон АЧХ и тем лучше будут характеристики фильтра. Все оно так, но вы забыли то, что каждый последующий каскад вносит свою лепту в ослабление сигнала.

В приведенных схемах мы строили АЧХ фильтра без внутреннего сопротивления генератора а также без нагрузки. То есть в данном случае сопротивление на выходе фильтра равняется бесконечности. Значит, желательно делать так, чтобы каждый последующий каскад имел значительно бОльшее входное сопротивление, чем предыдущий. В настоящее время каскадирование звеньев уже кануло в лету и сейчас используют активные фильтры, которые построены на ОУ.

Резюме

• Все электрические сигналы содержат смесь необходимых частотных компонентов и нежелательных частотных компонентов. Нежелательные частотные компоненты обычно вызваны шумом и помехами, и в некоторых ситуациях они отрицательно влияют на производительность системы.
• Фильтр – это схема, которая по-разному реагирует на разные части спектра сигнала. Фильтр нижних частот предназначен для пропускания низкочастотных компонентов и блокирования высокочастотных компонентов.
• Частота среза фильтра нижних частот указывает частотную область, в которой фильтр переходит от низкого затухания к существенному затуханию.
• Выходное напряжение RC фильтра нижних частот можно рассчитать, рассматривая схему как делитель напряжения, состоящий из (независимого от частоты) активного сопротивления и (зависимого от частоты) реактивного сопротивления.
• График амплитуды выходного сигнала (в дБ на вертикальной оси) в зависимости от частоты (в герцах в логарифмическом масштабе на горизонтальной оси) является удобным и эффективным способом проверки теоретического поведения фильтра (амплитудно-частотная характеристика). Вы также можете использовать график зависимости фазы выходного сигнала от частоты в логарифмическом масштабе, чтобы определить величину сдвига фазы, которая будет применяться к входному сигналу (фазо-частотная характеристика).
• Фильтр второго порядка обеспечивает более крутой спад; эта характеристика второго порядка полезна, когда сигнал не обеспечивает широкую полосу разделения между необходимыми частотными компонентами и нежелательными частотными компонентами.
• Вы можете создать RC фильтр нижних частот второго порядка, создав два идентичных RC фильтра нижних частот первого порядка, а затем подключив выход одного к входу другого. Итоговая частота –3 дБ будет ниже ожидаемой.

Оригинал статьи:

• Robert Keim. What Is a Low Pass Filter? A Tutorial on the Basics of Passive RC Filters

Заказ

Порядок фильтра описывает степень принятия или отклонения частот выше или ниже соответствующей частоты среза . Фильтр первого порядка, частота среза которого равна (F), представит ослабление 6 в первой октаве (2F), 12 дБ во второй октаве (4F), 18 дБ в третьей октаве (8F) и скоро. Если мы хотим узнать крутизну затухания фильтра, когда у нас есть отношение частот, выраженное в декадах (10F), соответствие будет 20 дБ / декада для первого порядка, 40 дБ для второго и т. Д. (всегда отображается в логарифмическом масштабе ).

Для выполнения аналоговых фильтров более высокого порядка обычно выполняется последовательное соединение фильтров 1-го или 2-го порядка, потому что чем выше порядок, тем сложнее фильтр. Однако в случае цифровых фильтров обычно получается более 100 порядков.